Research

Ci-dessous, un exposé très vulgarisé réalisé dans le cadre du concours “Ma thèse en 180 secondes”, qui donne une idée des thématiques abordées dans mes recherches. Pour en savoir plus, vous pouvez lire le texte qui suit la vidéo, conçu pour être accessible au plus grand nombre, avec des précisions supplémentaires pour ceux ayant suivi un cursus scientifique.

Les recherches que j’ai effectuées pendant ma thèse concernent principalement le rôle de la topologie, et dans une moindre mesure, du désordre, au sein de réseaux bidimensionnels d’atomes.

La topologie est une branche des mathématiques qui s’intéresse, entre autres, aux formes que prennent les objets de façon globale. Plus précisément, la topologie cherche à classer les objets, par exemple des surfaces, selon des propriétés qui sont invariantes sous des transformations continues. C’est-à-dire des transformations qui ne percent ni ne déchirent la matière — si l’on garde l’exemple des surfaces. Par exemple, le nombre de trous dans une surface est un invariant topologique : pour le modifier, on doit passer par une transformation non continue.

Elle a commencé à avoir une importance en physique de la matière condensée à partir des années 1980, lorsqu’une expérience de Klaus von Klitzing a montré qu’au sein d’un gaz d’électrons bidimensionnels refroidi à très basses températures et soumis à un champ magnétique intense, la résistance transverse était quantifiée : c’est-à-dire qu’elle prenait des valeurs entières.

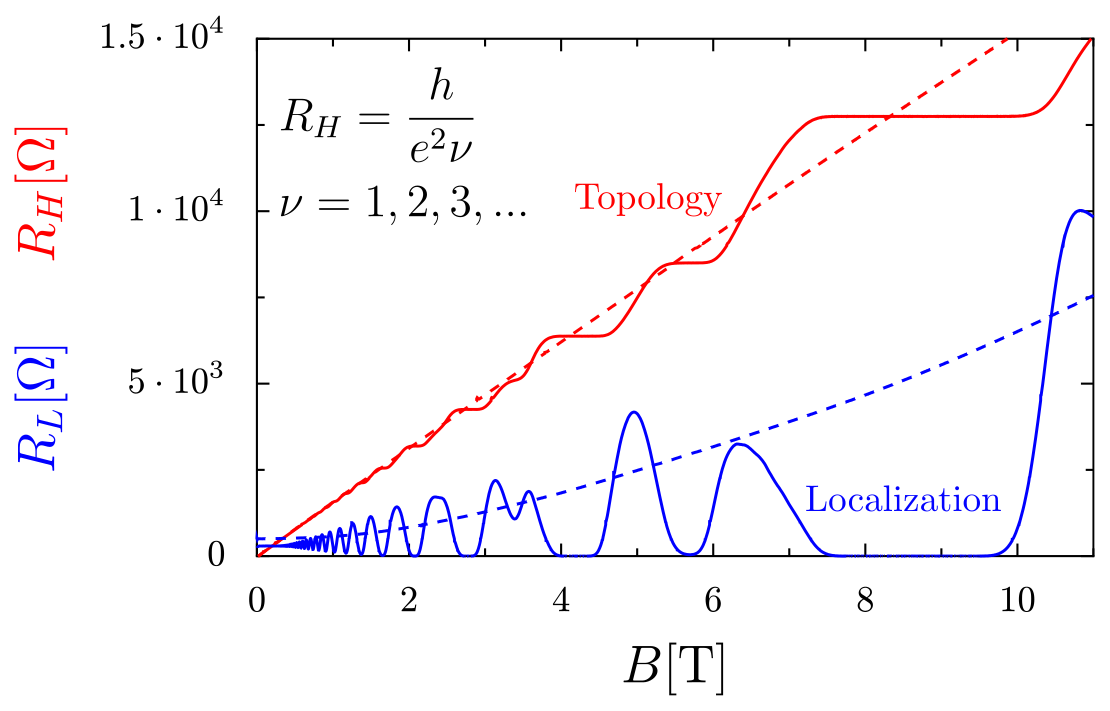
Très vite, on a soupçonné un comportement topologique pour expliquer cette quantification. À partir de cette expérience, plusieurs autres se sont développées, notamment pour obtenir à nouveau cette quantification, mais sans le champ magnétique, en utilisant par exemple le spin des particules.

Topologie en physique

La principale motivation étant que, dans les systèmes dits topologiques, il est souvent aisé de limiter les effets négatifs des imperfections ou des défauts. Ces derniers, constituant de petites perturbations continues, laissent invariantes certaines grandeurs comme la résistance ou la transmission.

Toute cette physique s’est d’abord développée pour les électrons, jusqu’à ce qu’une question se pose : peut-on faire de même pour les photons, les particules constituantes de la lumière ?

Les photons et le champ magnétique

À première vue, ce n’est pas si facile, car les trajectoires des photons ne semblent pas directement impactées par le champ magnétique. En effet, les photons sont dépourvus de charge et ne subissent donc pas la force de Lorentz, qui modifiait les trajectoires des électrons dans l’expérience de von Klitzing.

Cependant, il existe un moyen détourné : le champ magnétique peut modifier le milieu de propagation du photon. C’est le physicien Duncan Haldane qui va théoriser un nouveau concept : l’effet Hall quantique photonique. Cet effet sera démontré expérimentalement plus tard dans des réseaux constitués de cylindres de ferrites (voir Wang et al., 2009).

Mon travail de thèse

Par la suite, la question de la réalisation de cet effet dans des réseaux d’atomes froids s’est posée. Il s’agit d’atomes qui ne bougent pas, à travers lesquels la lumière se propage en interagissant avec eux (voir Perczel et al., 2017).

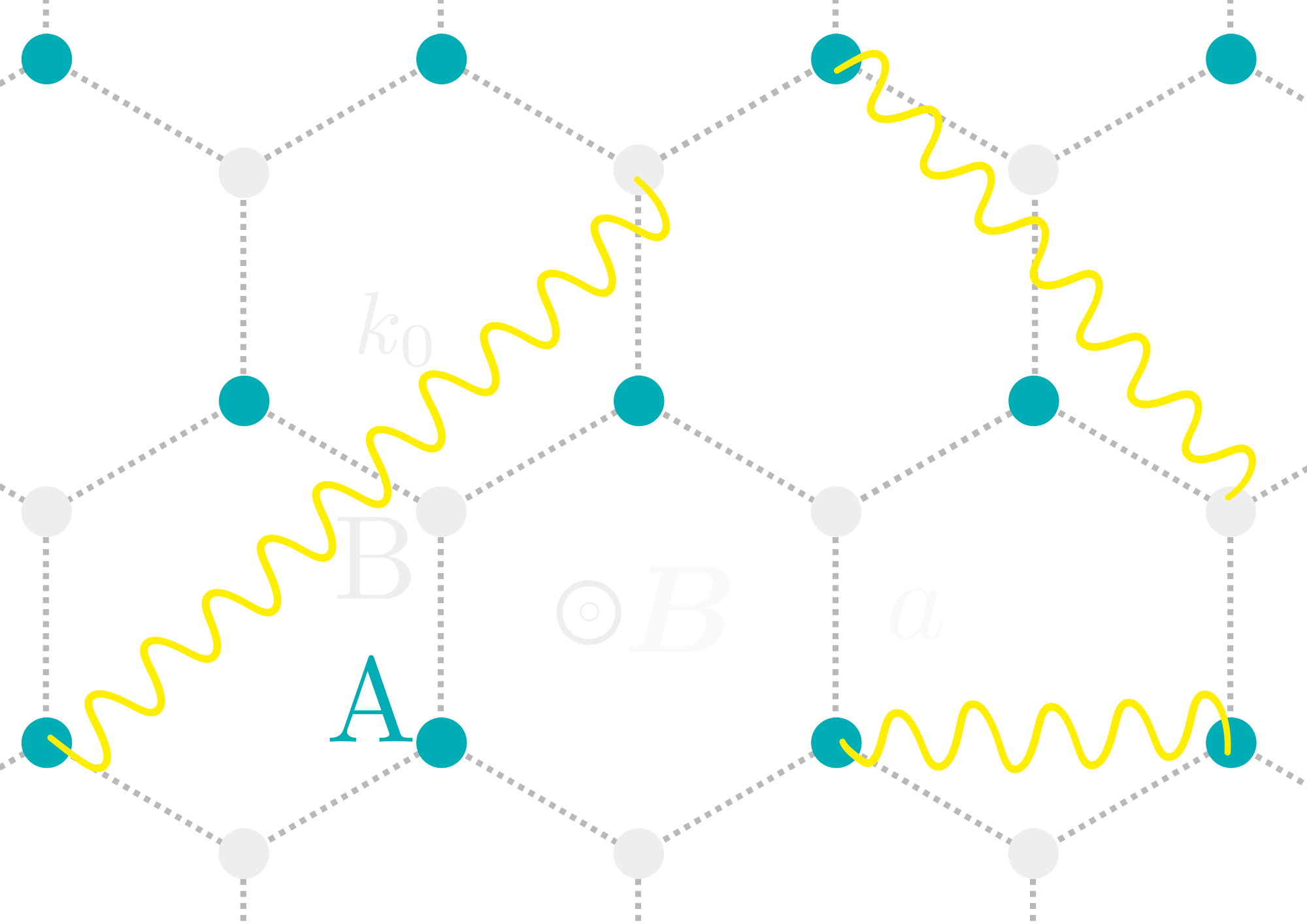
Mon travail de thèse s’inscrit dans ce contexte et tente de répondre aux questions suivantes :

• Comment peut-on contrôler la propagation de la lumière dans un réseau d’atomes 2D en nid d’abeille ?
• Quel est l’impact du désordre dans ce réseau ?
• Le désordre peut-il jouer un rôle bénéfique ?
• Est-il possible de contrôler la propagation de la lumière sans avoir recours à un champ magnétique ?
• Quelles expériences pouvons-nous réaliser pour valider ces modèles théoriques ?

Ma thèse a apporté des éléments de réponse à ces questions, que je vais tenter de vulgariser dans la suite.

La principale question que l’on se pose quand on étudie un échantillon d’atomes froids soumis à une excitation lumineuse, c’est de savoir si les photons vont être réémis ou pas, et si oui, à quelle fréquence.

Pour cela, il est important d’étudier l’ensemble des atomes comme un tout, un système connecté, car la physique d’un ensemble d’atomes diffère beaucoup de celle d’un seul atome et diffère aussi de la somme des atomes. Comme l’a dit un grand physicien :

“Plus, c’est différent” (voir “More is Different” par Philip Warren Anderson).

Je me suis donc d’abord intéressé à quantifier précisément les limites dans lesquelles les photons sont réémis ou non et comment cela se produit lorsque le système est soumis à un champ magnétique. En termes techniques, on dit qu’on étudie la “largeur de gap”, c’est-à-dire la zone dans laquelle les photons ne sont pas réémis.

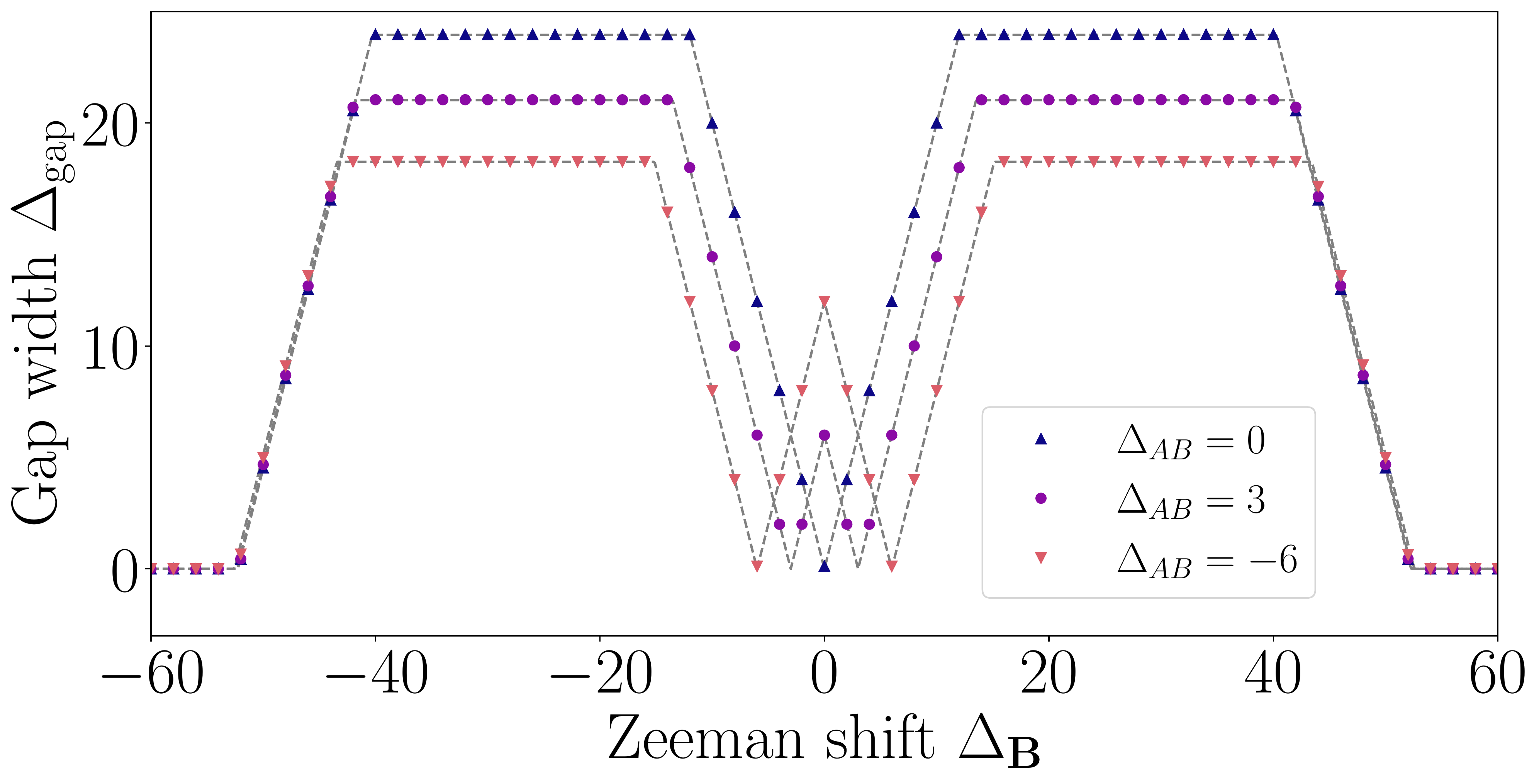
Déterminer avec précision la largeur de gap d’un système est important pour pouvoir l’utiliser dans des applications industrielles. Pouvoir contrôler cette largeur de gap l’est encore plus. C’est ce qui est fait dans les semi-conducteurs, qui sont à la base de nombreuses technologies modernes. Dans notre cas, le champ magnétique est un paramètre de contrôle du gap.

Ensuite, on veut savoir si ce gap va continuer d’exister si notre système est abîmé ou subit des défauts. Il est apparu très vite que les propriétés topologiques de notre système lui permettaient de résister à un désordre très élevé. Plus tard, il a été possible de montrer que, dans certaines conditions, l’ajout de désordre permettait lui aussi de créer un gap. C’est ce qu’on appelle l’isolant topologique d’Anderson.

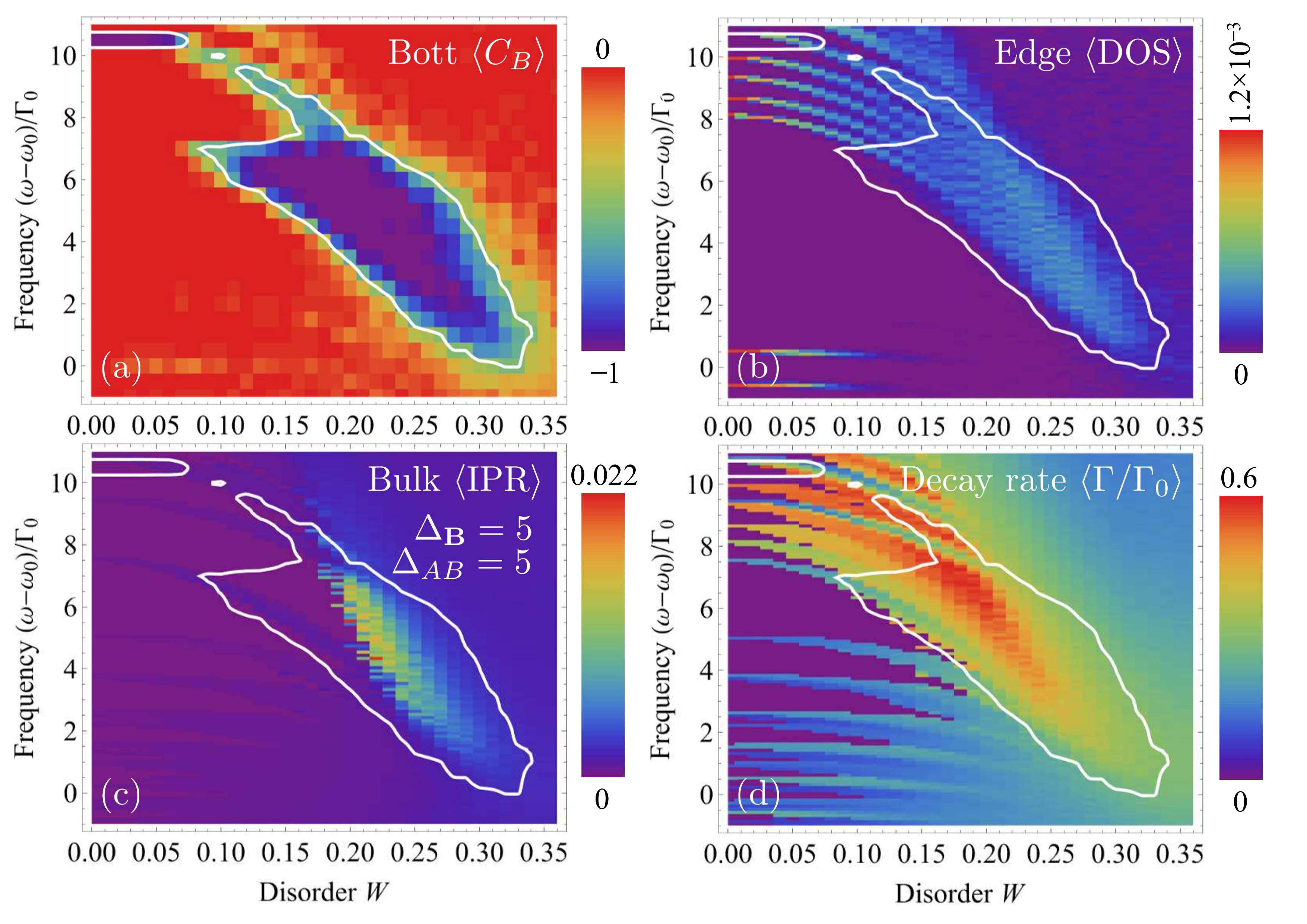
Nous avons ensuite cherché à recréer le même type de physique sans utiliser de champ magnétique. Cela a fonctionné, et nous avons pu étudier l’impact du désordre dans ces systèmes en collaboration avec une équipe d’expérimentateurs à Nice.

Se passer de champ magnétique pour créer un système topologique est intéressant d’un point de vue des applications industrielles, car il n’est pas possible d’avoir sur toutes les puces photoniques des champs magnétiques intenses.

Pour répondre à toutes ces questions, ce sont principalement des modélisations numériques que j’ai effectuées. Les atomes sont considérés comme des points et on modélise la propagation de la lumière en leur sein.

D’un point de vue un peu technique, il s’agit soit de trouver les vecteurs propres du Hamiltonien du système, soit de résoudre les équations de Maxwell à l’aide d’une simulation éléments finis.

Dans ma thèse, j’ai aussi étudié, un peu comme un projet annexe, la topologie dans des modèles un peu plus simples, des modèles jouets comme les modèles de tight-binding, où les interactions se font uniquement entre plus proches voisins. Ces systèmes sont plus simples à résoudre mais peuvent néanmoins modéliser des situations réelles, comme l’expérience des cylindres diélectriques du groupe de Fabrice Mortessagne (voir par exemple le travail d’Alberto Razo-Lopez).

En plus du nombre de Chern, un invariant topologique bien connu, j’ai calculé l’indice de Bott, un invariant topologique en espace réel, pour identifier les phases topologiques quand j’étudiais des systèmes désordonnés.

À cette occasion, j’ai développé un petit package Python disponible ici : PyBott.