Topology in tight-binding models
Introduction

The honeycomb lattice


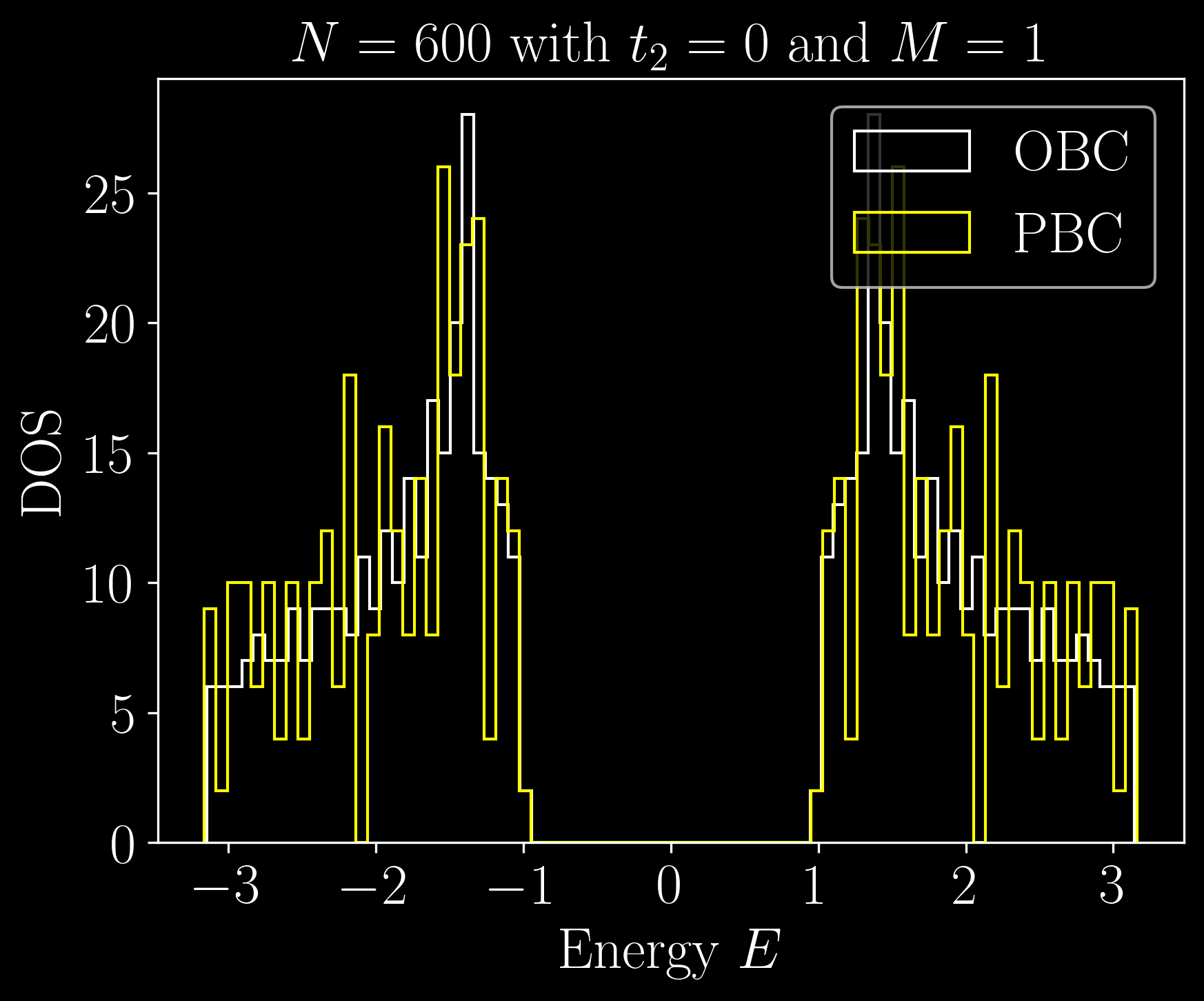
OBC


PBC
The Haldane model
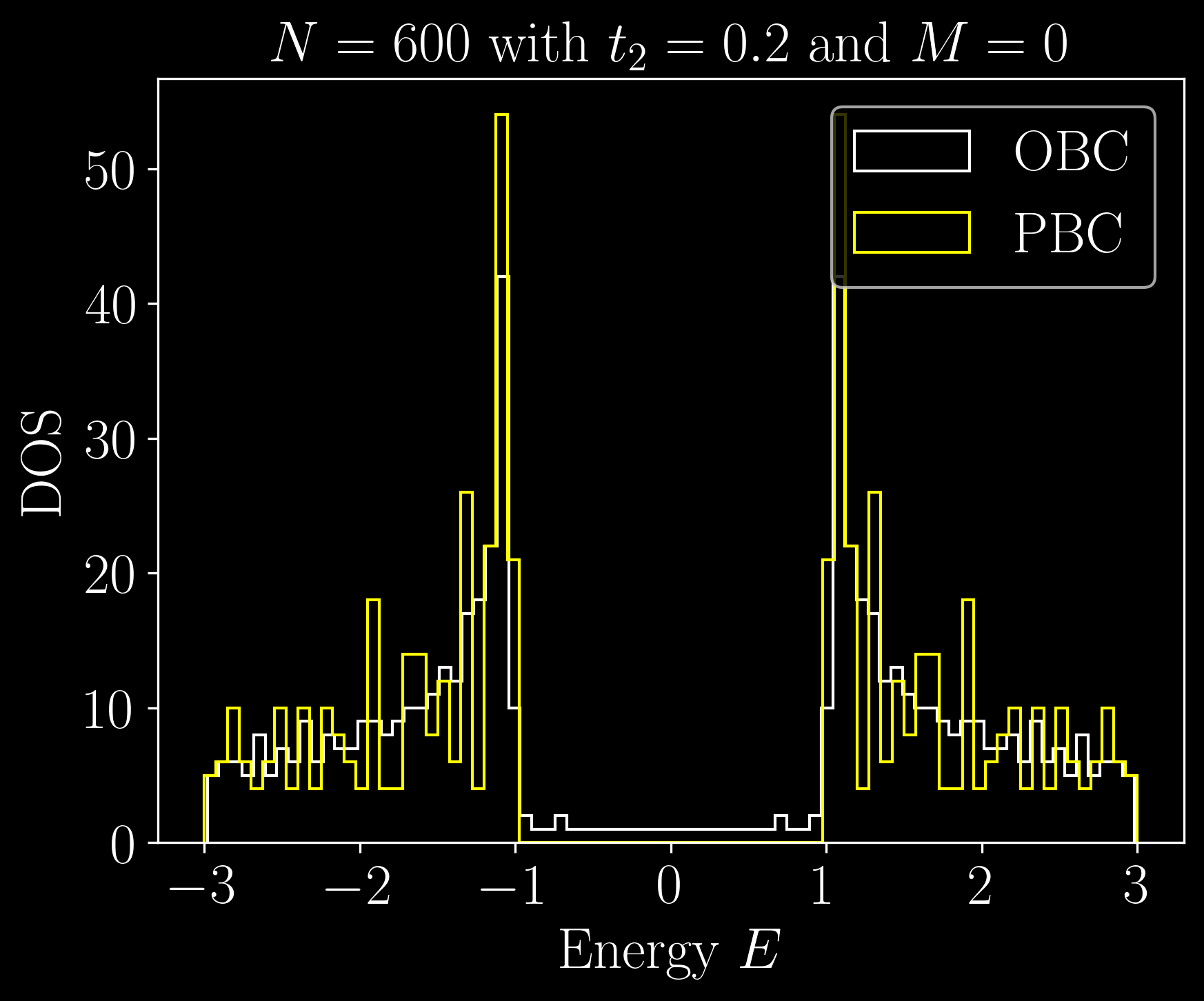
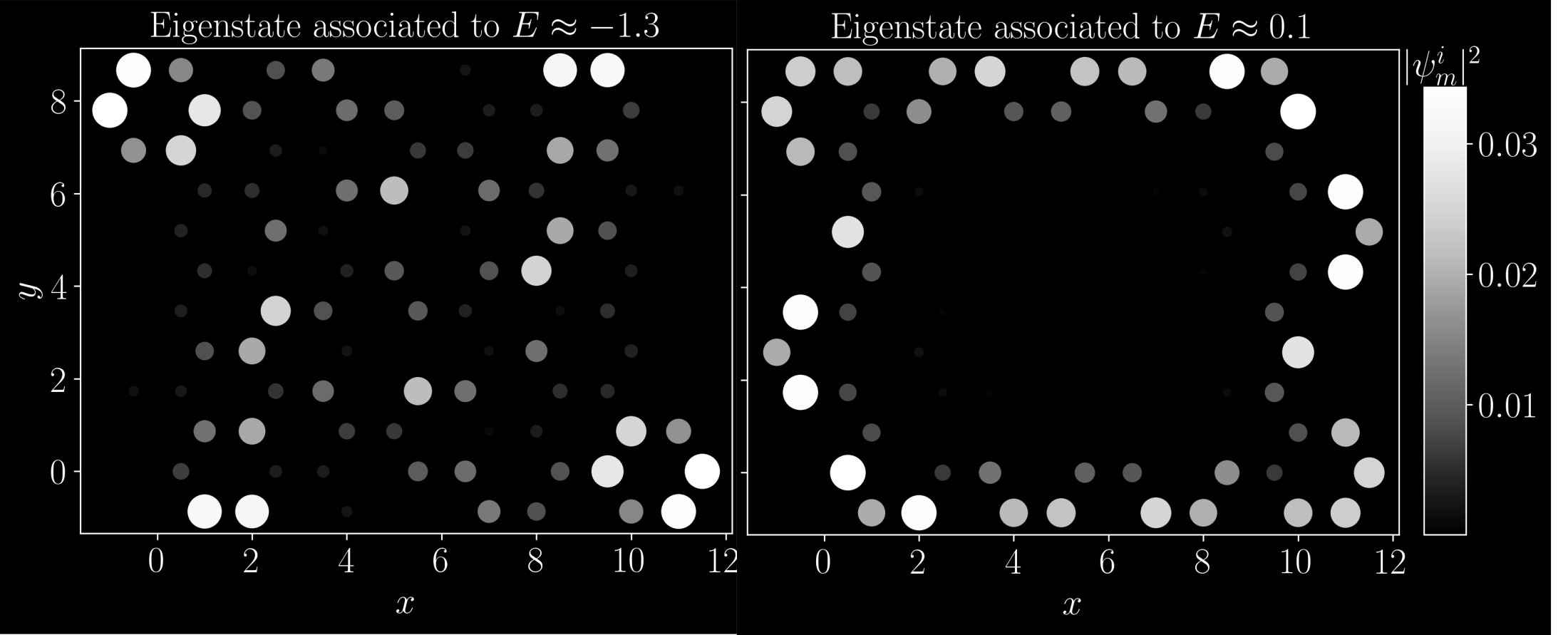
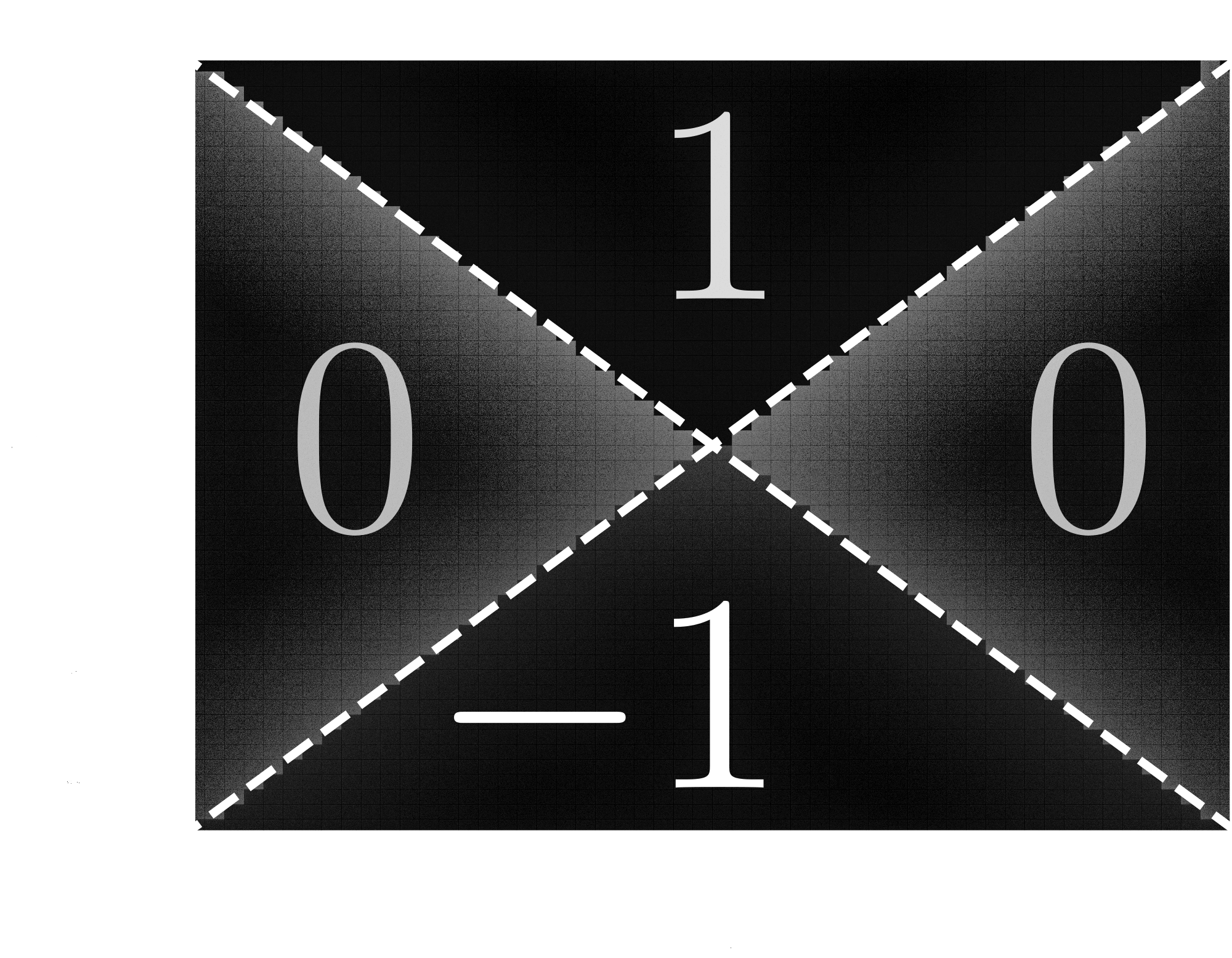

The Kekule model



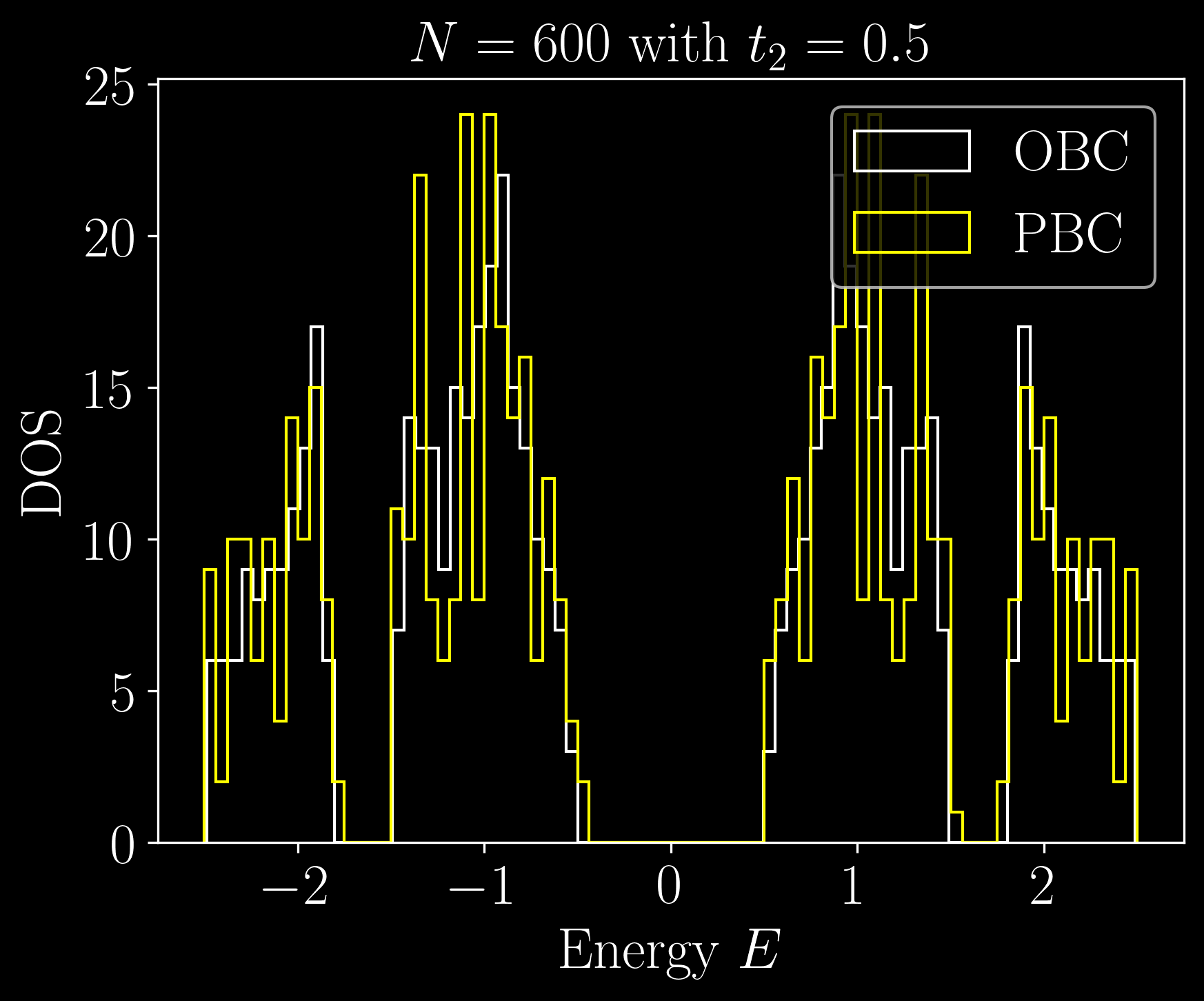
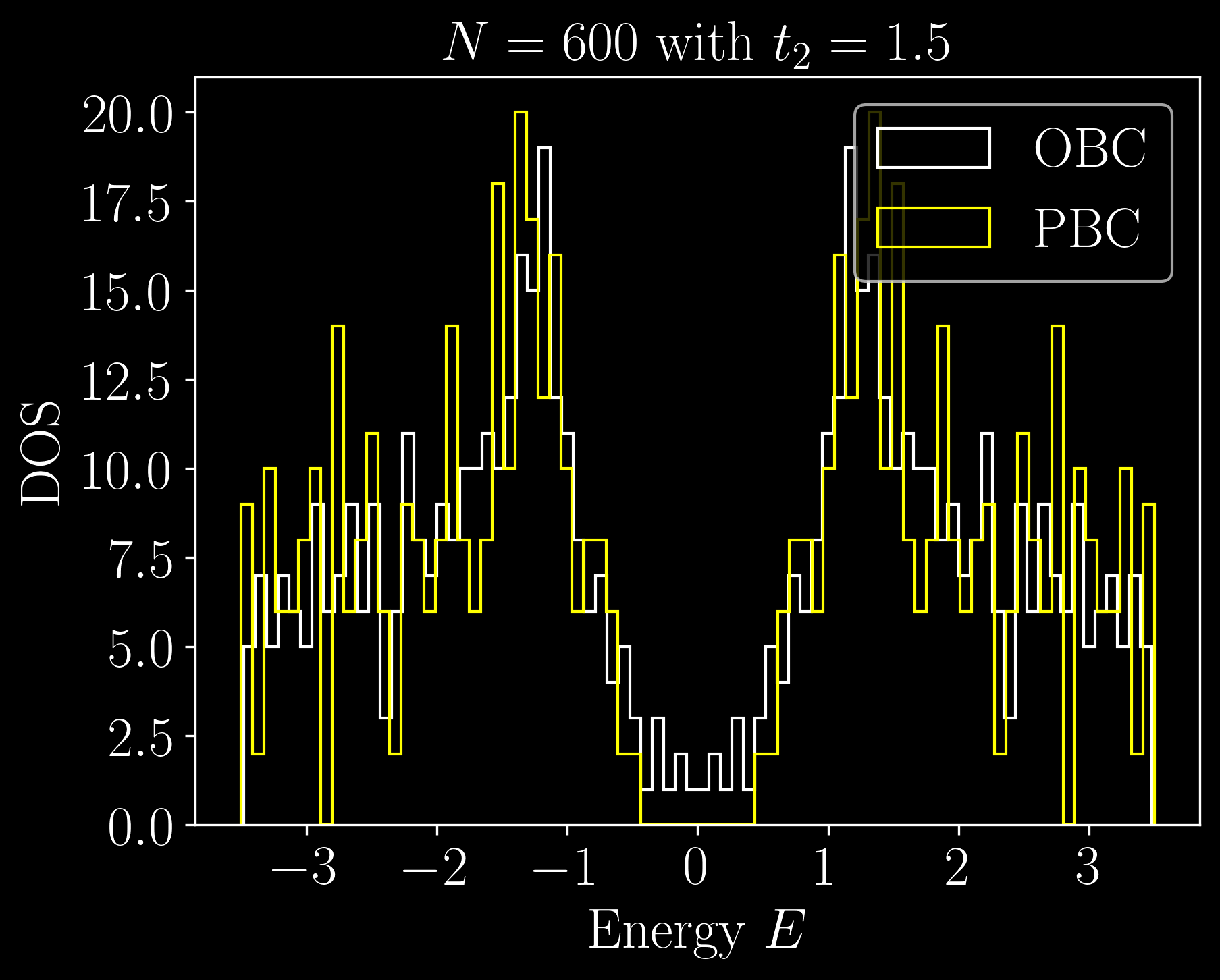
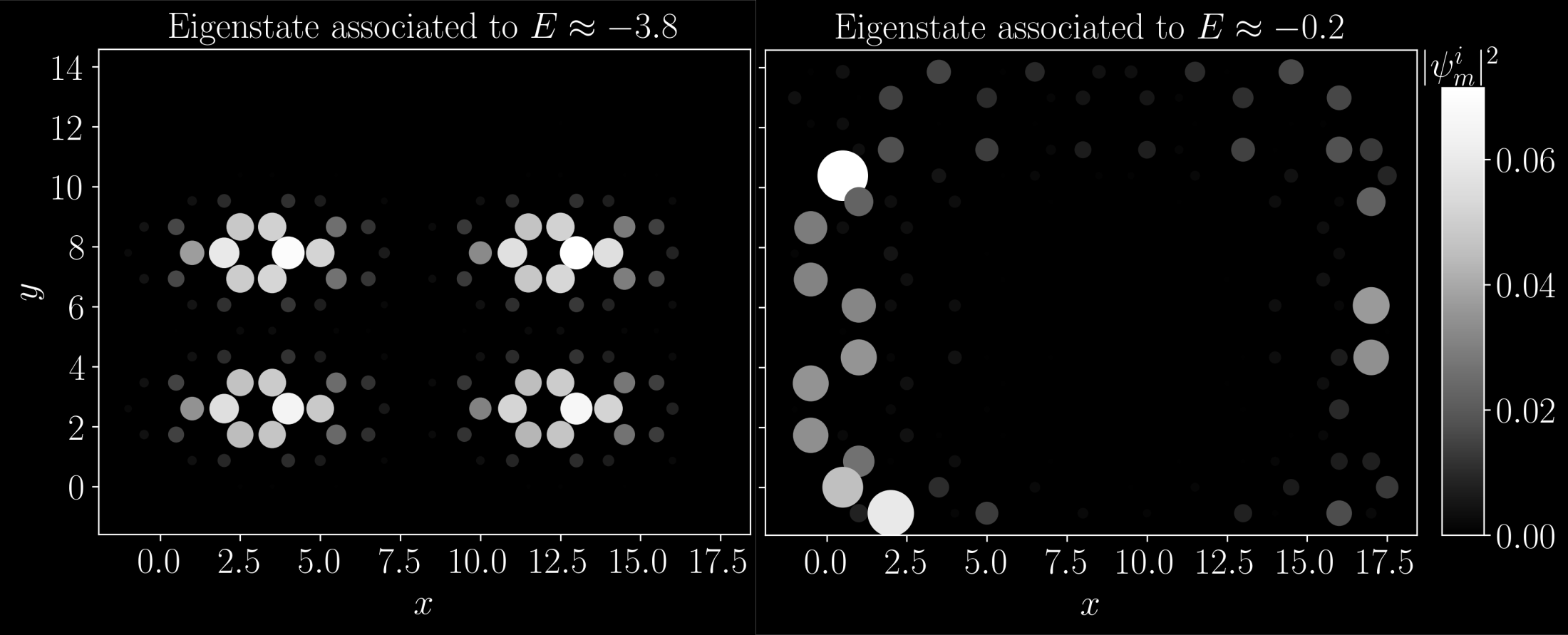
We consider only one cell: \[ H = t_1 \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 1\\ 1 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 1\\ 1 & 0 & 0 & 0 & 1 & 0\\ \end{pmatrix} \]
We build wave functions carrying the pseudospins \begin{align*} p_{\pm} &=& p_x \pm i p_y \\ d_{\pm} &=& d_{x^2-y^2} \pm i d_{xy} \end{align*}
From which we are able to build the operator $\sigma$ \[ \sigma = \mathbb{1}_{N_{\textrm{cluster}}}\otimes Q\begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}Q^{-1} \] where $Q=(s\; p_+\; p_-\; d_+\; d_-\; f)$
We can now define a new Hamiltonian \[ H' = P\sigma P \]
From which we can split the pseudo-spins up and down: \[ H' = H_+\oplus H_- \]
And define a new topological invariant, the Spin Bott Index: \[ C_{\textrm{SB}} = \frac{C_+ - C_-}{2} \]
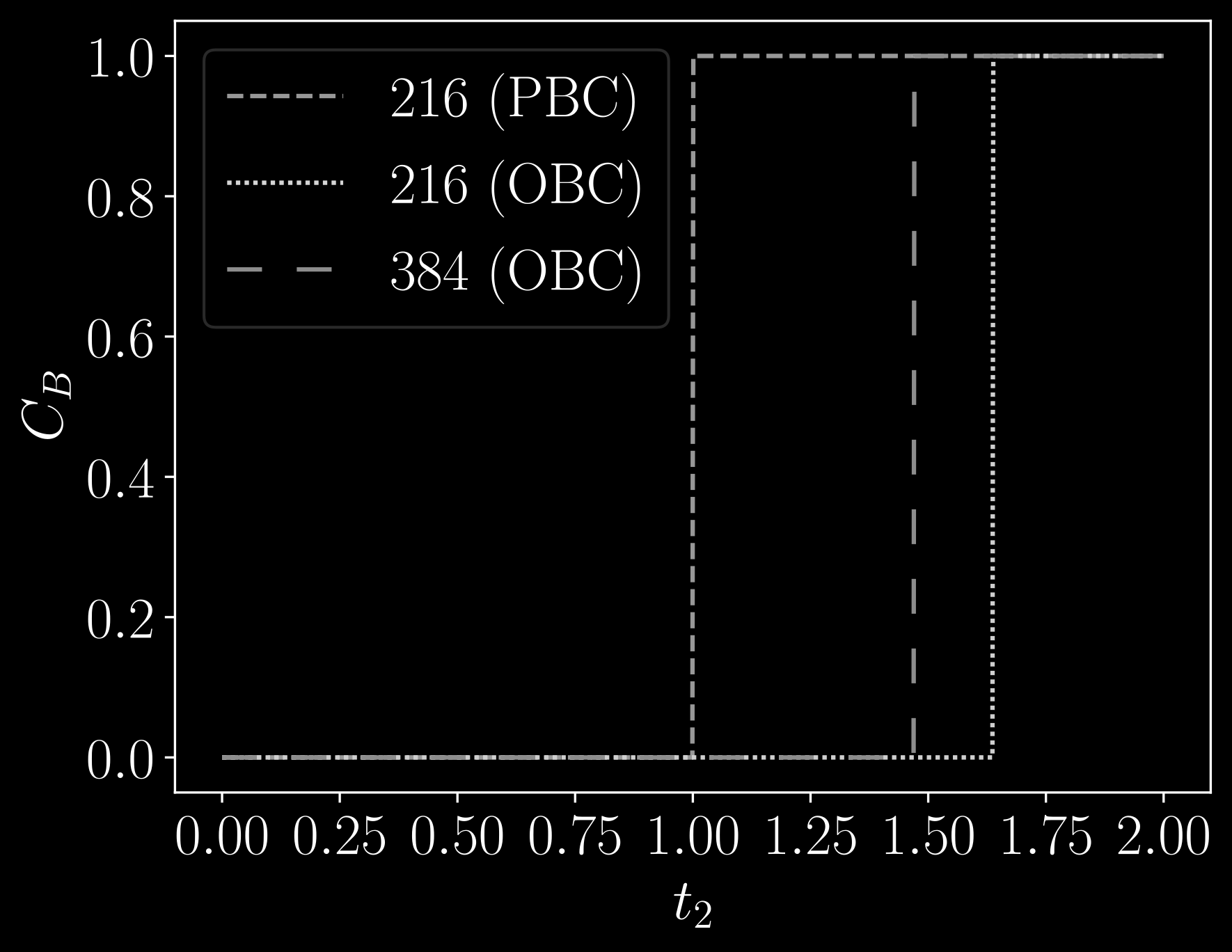
Going further
Reducing the size of the system:
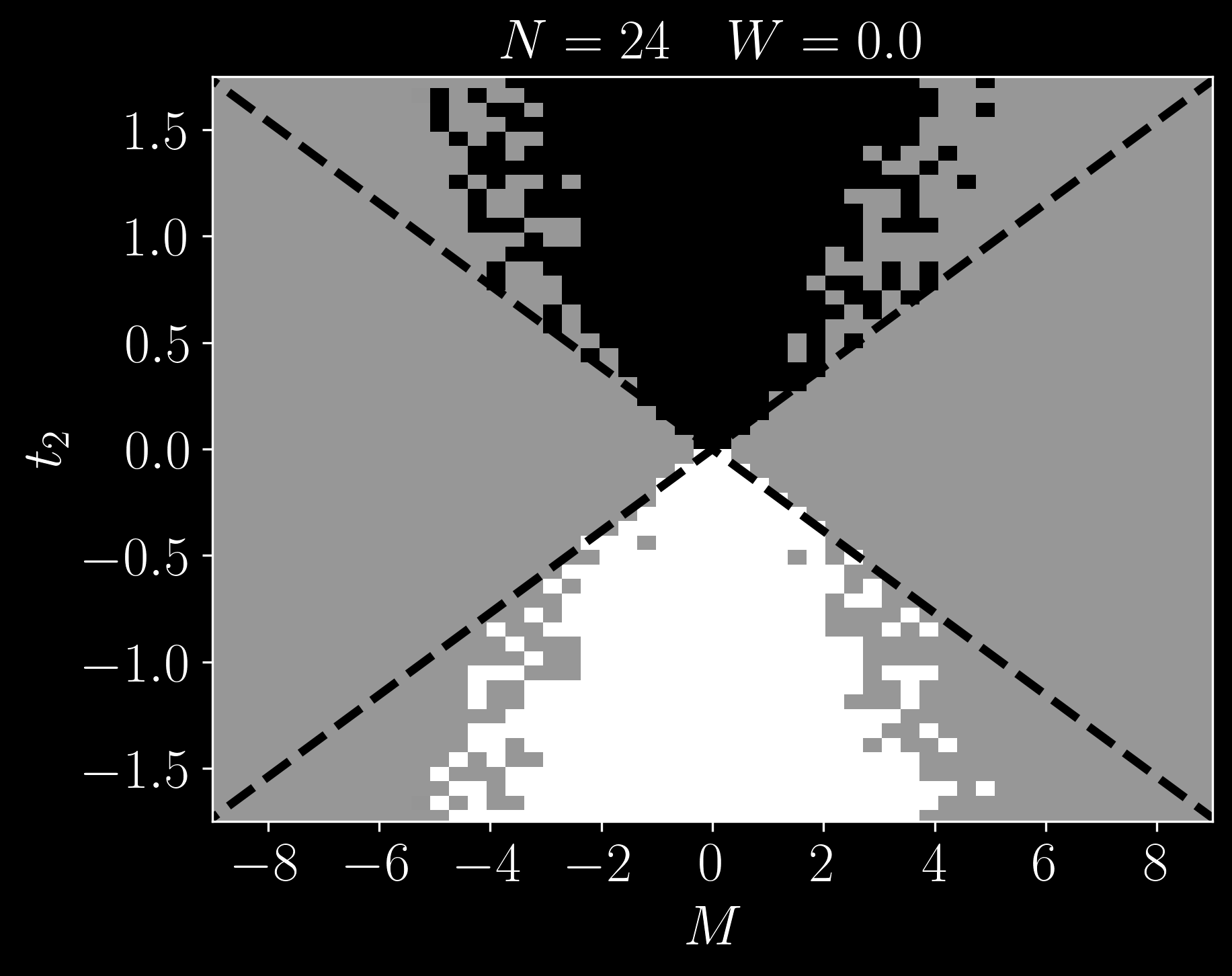
\[ H' = H_{\textrm{Haldane}} + \sum_i w_i c_i^\dagger c_i \]
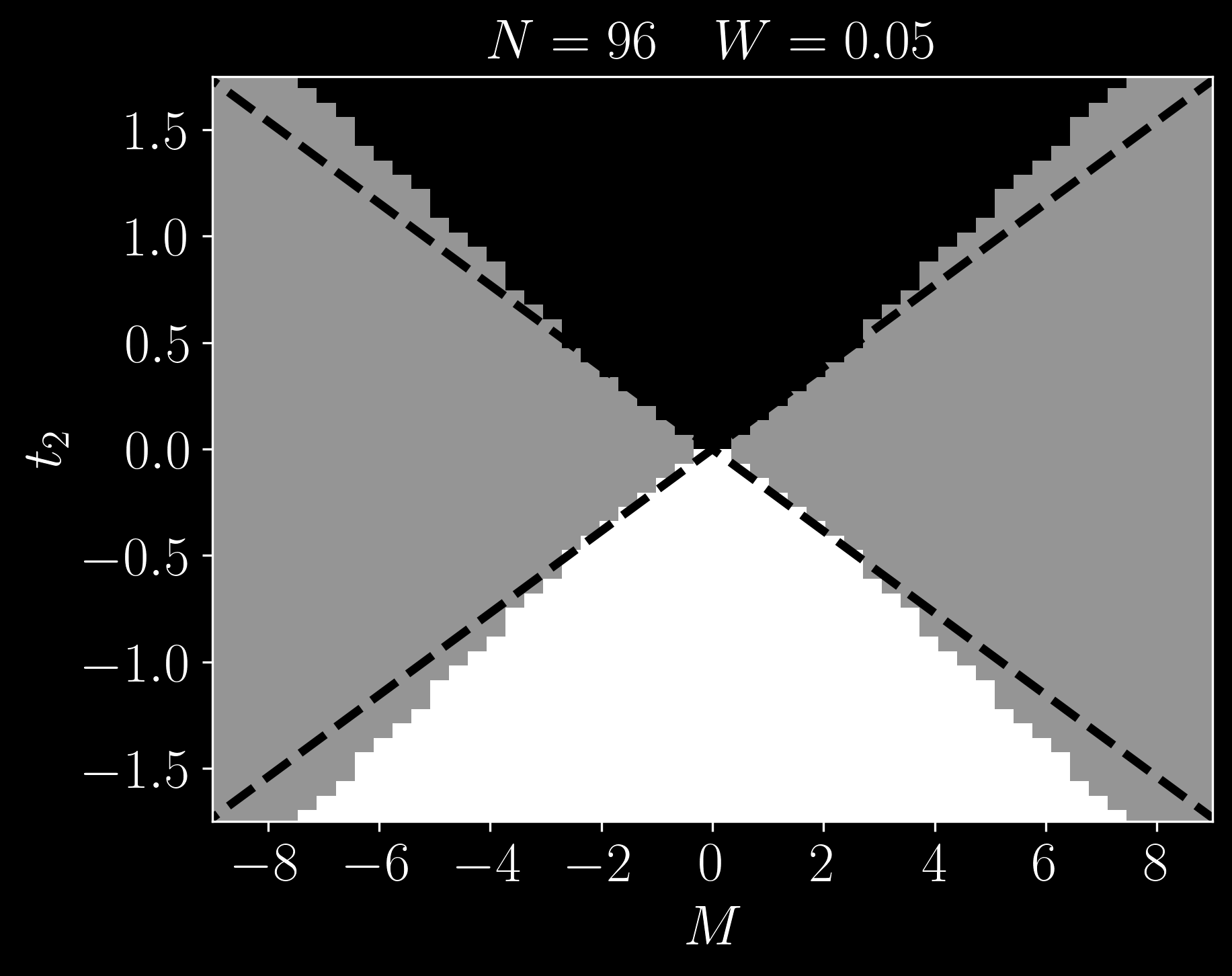
Take away message
- Mobility gap
- Topological VS trivial
- Topological invariant in real space, robust to disorder
- Link with commuting matrices
Bibliography
- Hastings and Lorings: Topological insulators and $C^*$-algebras
- Daniele Toniolo: On the Bott index of unitary matrices on a finite torus
- D. Haldane: Model for a Quantum Hall Effect without Landau Levels
- Wu and Hu: Topological Properties of Electrons in Honeycomb Lattice with Kekulé Hopping Textures