Topological photonics in two-dimensional atomic lattices
Pierre Wulles
Supervision of Dr. S. E. Skipetrov
Grenoble 24/09/2024
The quantum Hall effect
Image 1 Image 2
New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance K. v. Klitzing et al., PRL. 1980
A quantized resistance
M Flöser et al. 2013 New J. Phys. 15 083027
Is it possible to reproduce this effect with photons ?


Electrons...
  • Obey Fermi statistics
  • Experience the Lorentz Force
  • Are not absorbed



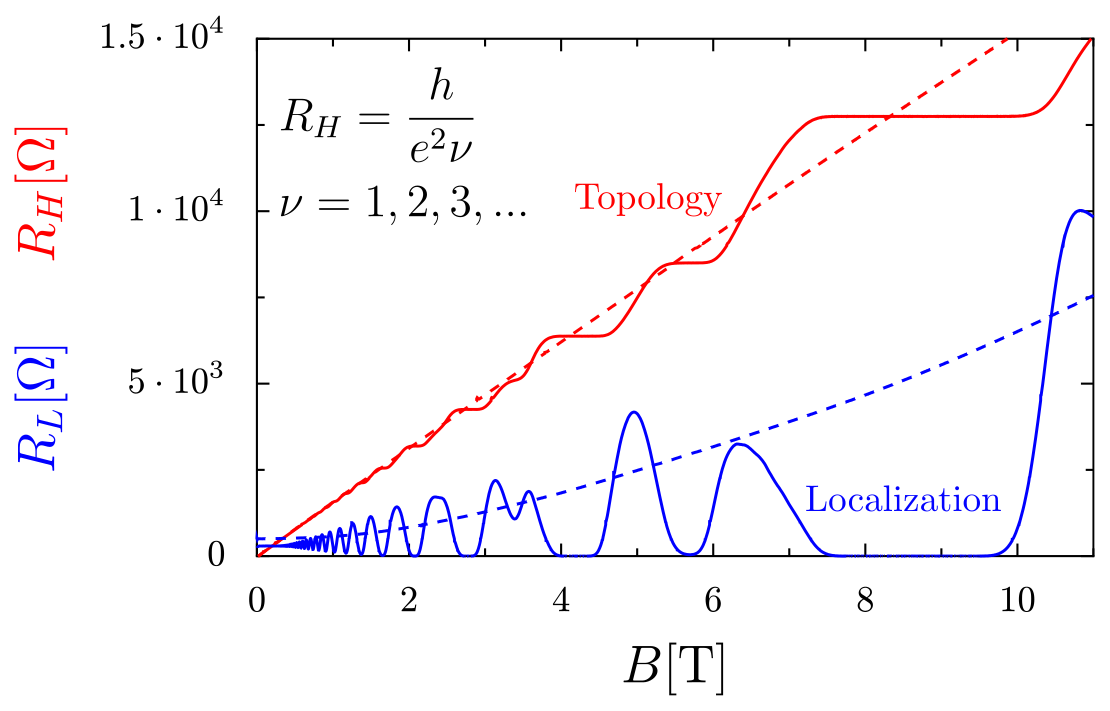
But the magnetic field affects the material properties!
Topological photonics through history
  • Quantum Hall Effect (K. v. Klitzing) 1980
  • 1988Quantum anomalous Hall effect (D. Haldane)
  • 2005Photonic Quantum Hall effect
       (D. Haldane & S. Raghu)
  • Photonic Quantum Hall effect (Wang et al.)2008
  • 2017Topological quantum optics (Perczel et al.)
Goal: reproduce an analog of the quantum Hall effect with cold atoms.
  • Topological Quantum Optics in Two-Dimensional Atomic Arrays, J. Perczel et al., PRL 119, 2017
  • Photonic band structure of two-dimensional atomic lattices J. Perczel et al., PRA 96, 2017
  • Topological properties of a dense atomic lattice gas, R. J. Bettles et al., PRA 96, 2017
The quantum spin Hall effect (2007)
Topology in a cup of tea
Topology is the branch of mathematics originally used to classify the shapes of three-dimensional objects such as soccer balls, [...] These original ideas of topology were greatly generalized and made abstract by mathematicians, but the central idea, that things are only “topologically equivalent” if they can smoothly be transformed into each other, remains as its key idea.
— D. Haldane 2016
Genus
Curvature
The link between genus and curvature is made by the Gauss-Bonet formula

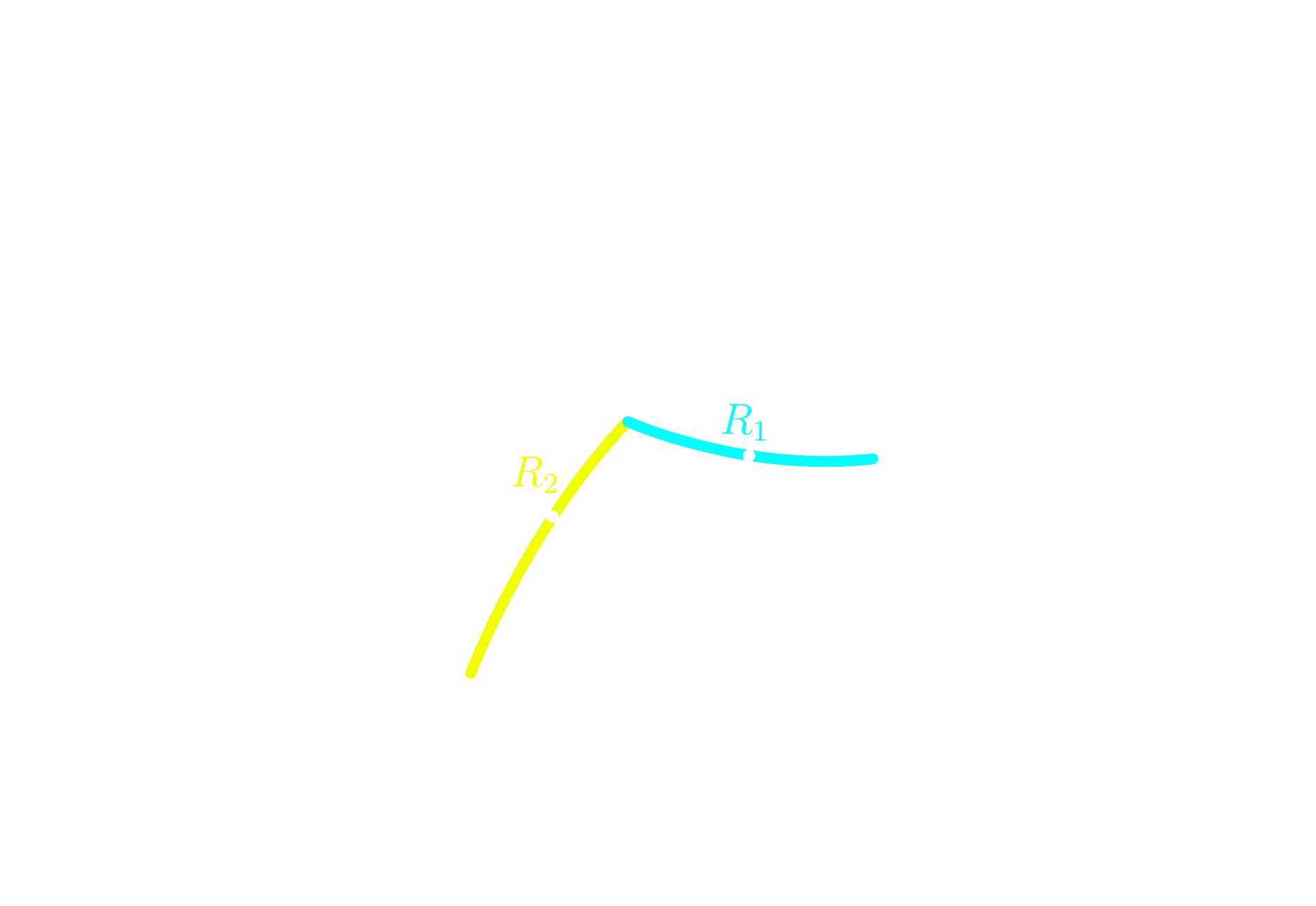
$$\int_S \Omega (\mathbf{x}) \mathrm{d}^2 \mathbf{x} = 4 \pi (1 - g)$$

  • Surfaces can be classified using their genus
  • Only smooth transformations are allowed in a characteristic class
  • Curvature helps for computing topological invariants
The Haldane Model
$$\hphantom{\begin{align*} H &= t_1\sum_{\langle i,j \rangle} c_i^\dagger c_j\\ &+ it_2\sum_{\langle\langle i,j \rangle\rangle}\sigma_{ij} c_i^\dagger c_j\\ &+ \sum_{i}M_ic_i^\dagger c_i \end{align*}}$$
$$\begin{align*} H &= t_1\sum_{\langle i,j \rangle} c_i^\dagger c_j + it_2\sum_{\langle\langle i,j \rangle\rangle}\sigma_{ij} c_i^\dagger c_j + \sum_{i} M_i c_i^\dagger c_i \\ \sigma_{ij} &= \pm 1 \quad\textrm{(Breaks TRS)}\end{align*}$$
Band structure of Haldane model for $t_2=M=0$
Band structure of Haldane model for $t_2=M=0$
The Chern number
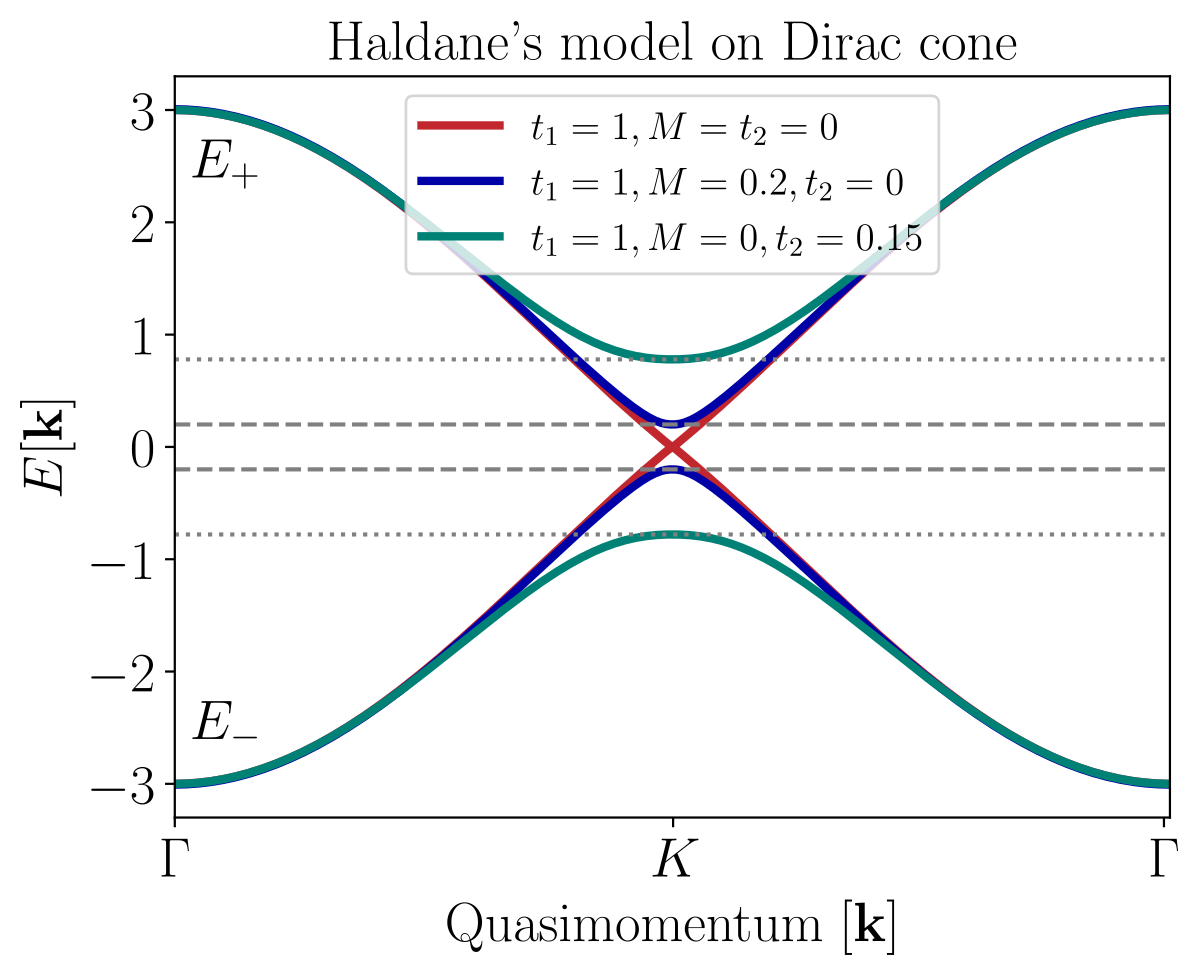
  • Every eigenstate can be written as: $$\bm{\psi}_{m,\bm{k}} (\bm{r})=\exp(i\bm{k}\cdot\bm{r})\bm{u}_{m,\bm{k}}(\bm{r})$$

  • Berry connection:$$ \bm{A}_m (\bm{k}) = i \langle \bm{u}_{m,\bm{k}} (\bm{k}) | \nabla_{\bm{k}} | \bm{u}_{m,\bm{k}} \rangle $$

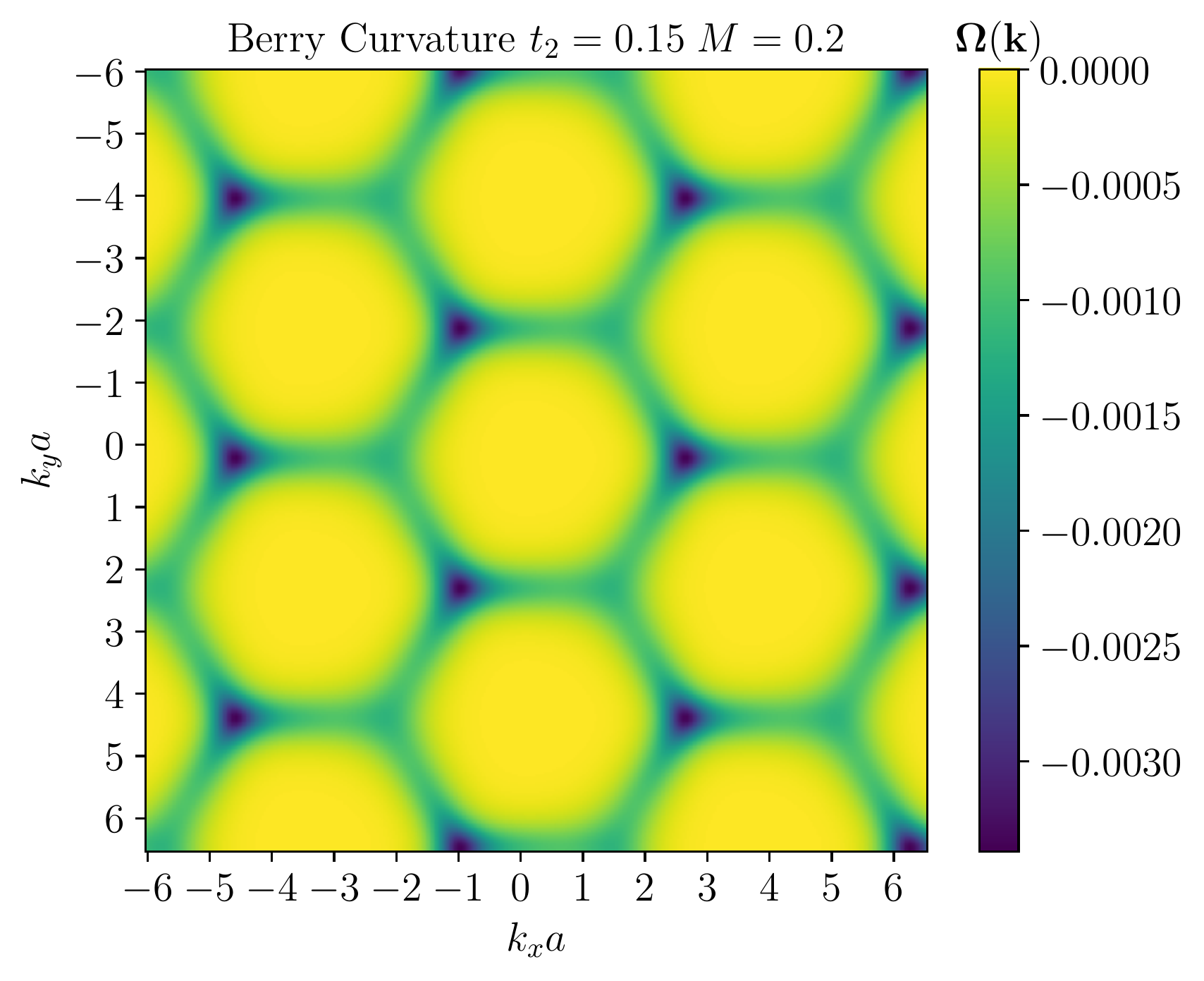
  • Berry curvature:$$ \bm{\Omega}_m (\bm{k}) = \bm{\nabla} \times \bm{A}_m(\bm{k}) $$

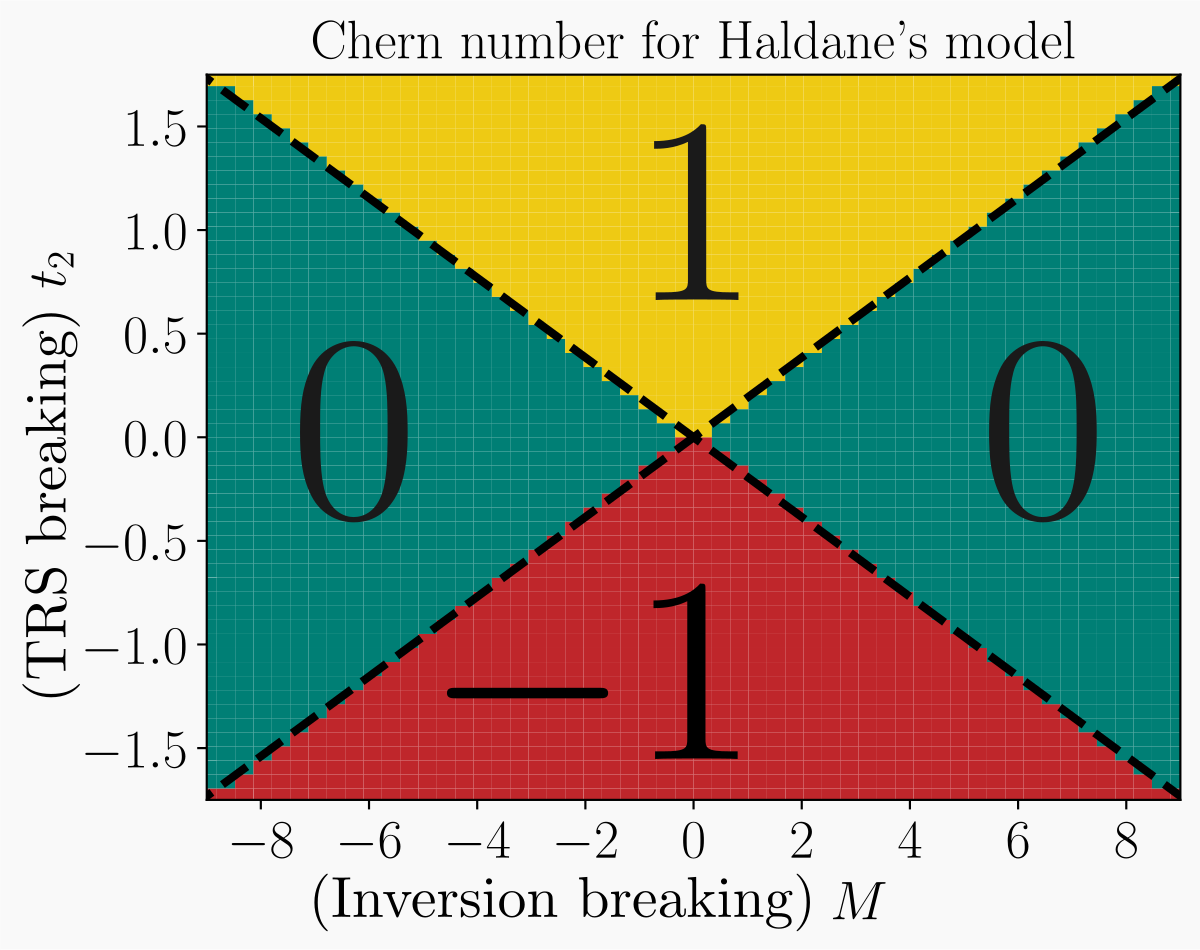
  • Chern number:$$C_m = \frac{1}{2 \pi i} \int_{\mathbb{T}^2} \bm{\Omega}_m (\bm{k}) \mathrm{d}^2 \bm{k} \in \mathbb{Z} $$

What are the physical consequences of a non-zero Chern number?
Infinite nanoribbon
The bulk-edge correspondence
Image 1 Image 2
Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly", D. Haldane, PRL. 61. 1988
Open Boundary Conditions

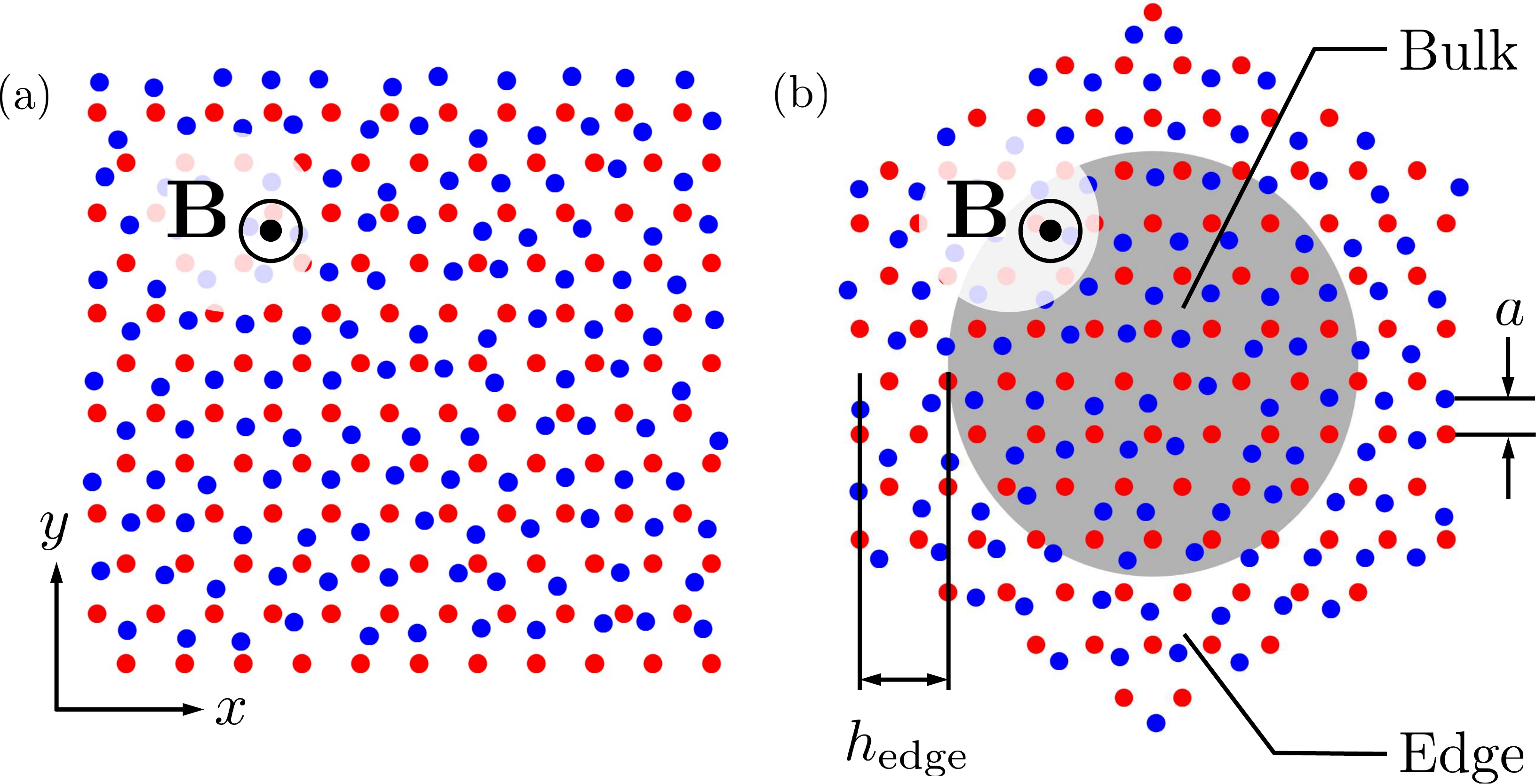
Periodic Boundary Conditions
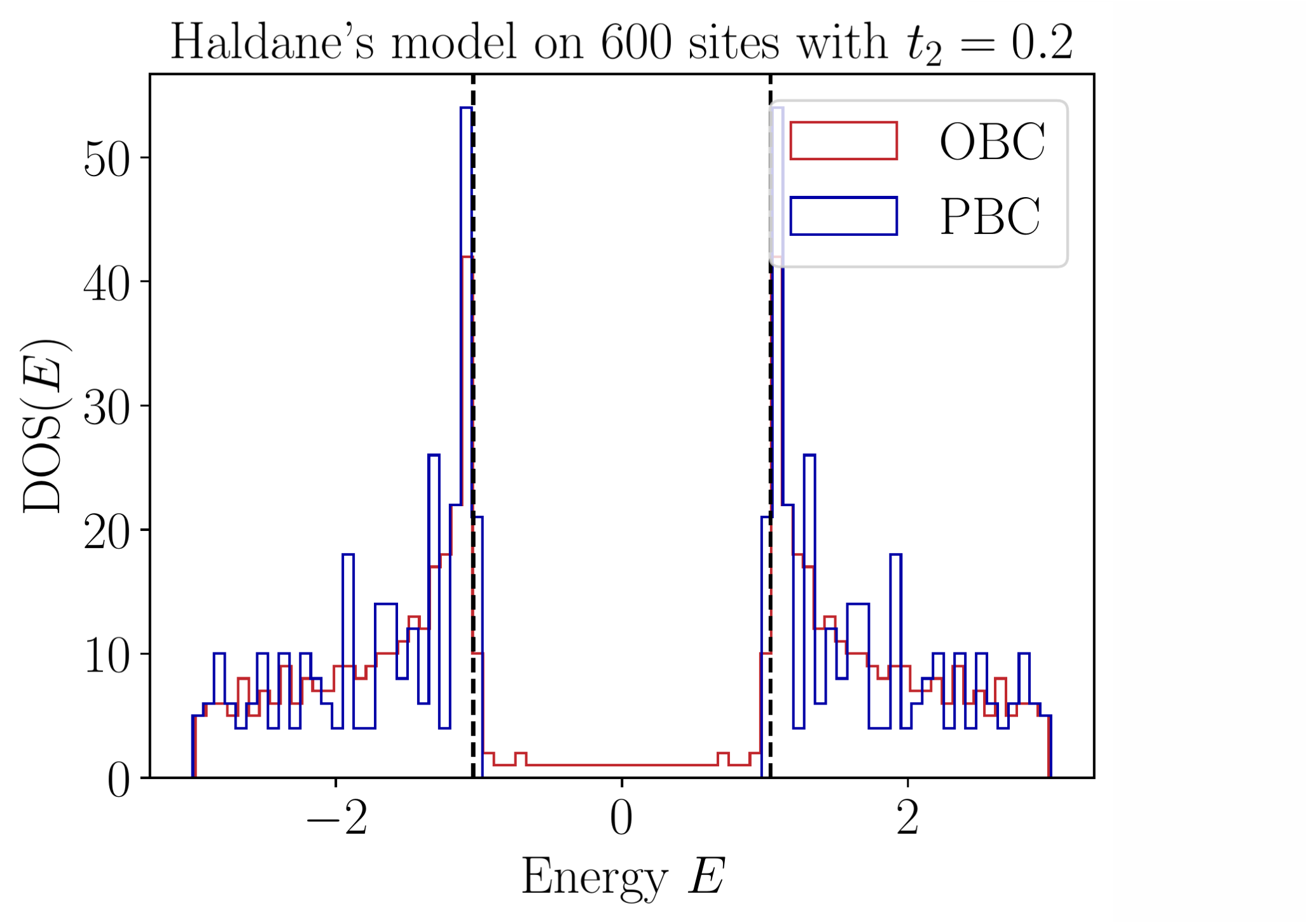
  • Density of states: $$\textrm{DOS}(E) = \sum_i \delta(E-E_i)$$
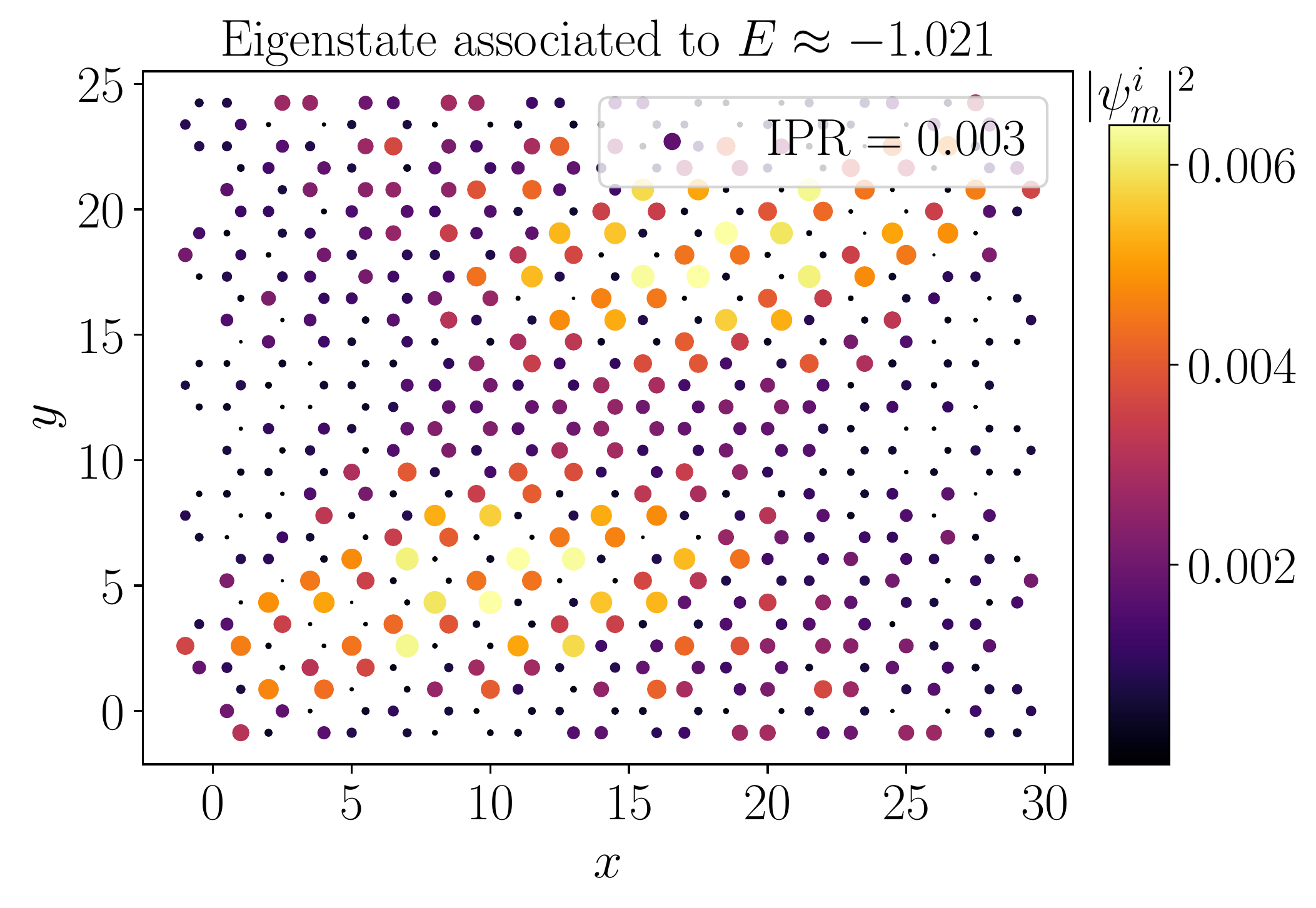
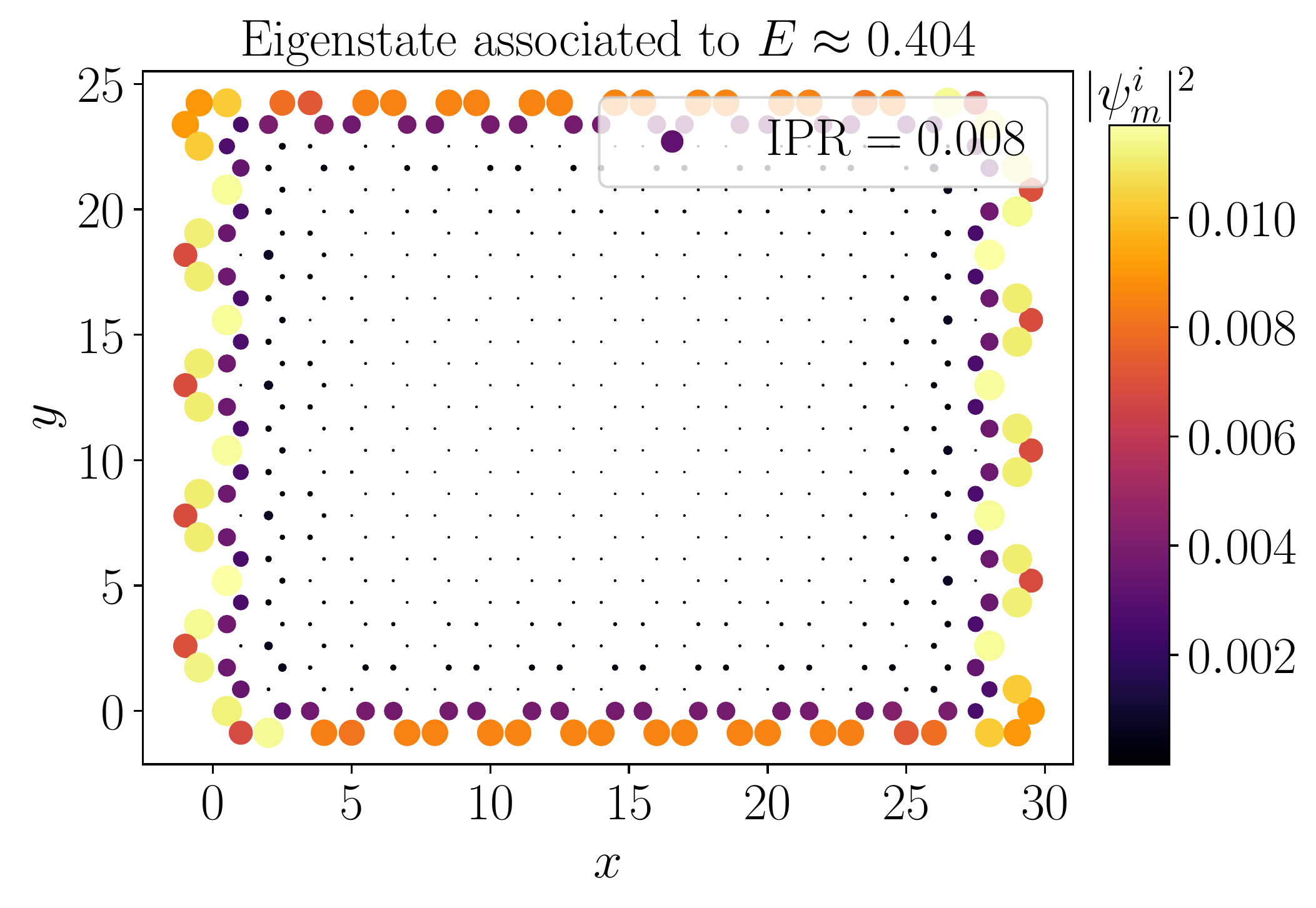
  • Inverse Participation ratio: $$\textrm{IPR} (m) = \frac{\sum_{i = 1}^N | \psi_m^{(i)} |^4}{\left( \sum_{i = 1}^N | \psi_m^{(i)} |^2 \right)^2}$$
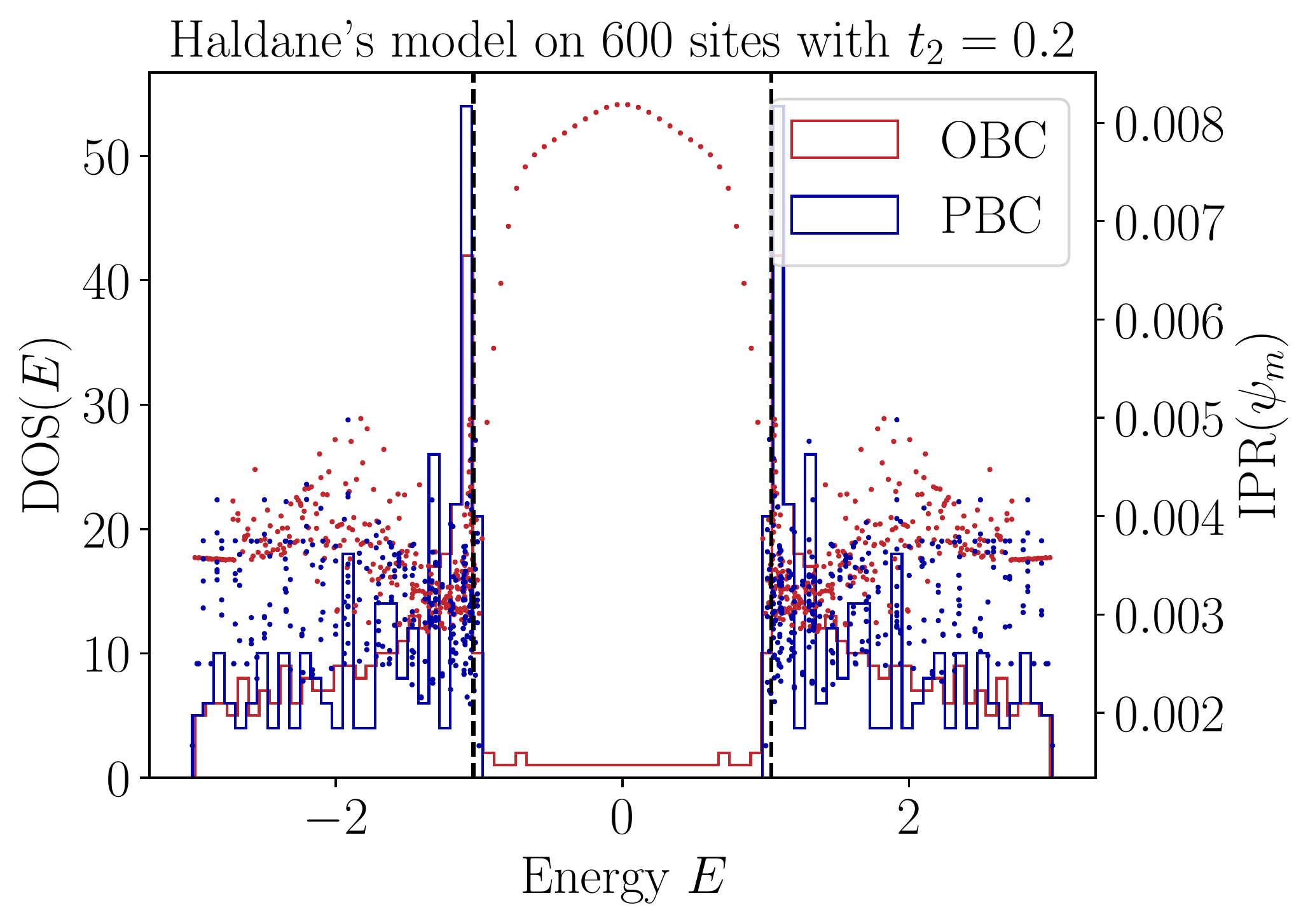
  • Density of states: $$\textrm{DOS}(E) = \sum_i \delta(E-E_i)$$
  • Inverse Participation ratio: $$\textrm{IPR} (m) = \frac{\sum_{i = 1}^N | \psi_m^{(i)} |^4}{\left( \sum_{i = 1}^N | \psi_m^{(i)} |^2 \right)^2}$$
Image 1 Image 2
What are alternative topological invariants to the Chern number in real space?

  • Mapping topological order in coordinate space R. Bianco and R. Resta PRB 84, 241106(R) – 13/12/2011
  • A Guide to the Bott Index and Localizer Index Terry A. Loring, arxiv, 2019
  • Disordered topological insulators via C*-algebras Terry A. Loring and M. B. Hastings, EPL Vol. 92, 2010
  • Position matrices: \[ X = \textrm{diag} (x_1, \ldots, x_n) \quad Y = \textrm{diag} (y_1, \ldots, y_n) \]
  • $(\mathbf{q}_1, \ldots, \mathbf{q}_m)$ generates the subspace below the Fermi level $E_F$, we define: $$ W = [\bm{q}_1 \ldots \bm{q}_m]$$
  • Projection operators on $x$ and on $y$: \[ U = W^{\dagger} \exp \left( i \frac{2 \pi}{L_x} X \right) W\quad V = W^{\dagger} \exp \left( i \frac{2 \pi}{L_y} Y \right) W \]
Finally we define the Bott index as:
\[ C_B = \frac{1}{2 \pi} \textrm{Im} (\textrm{tr} (\log (VUV^{- 1} U^{- 1}))) \]

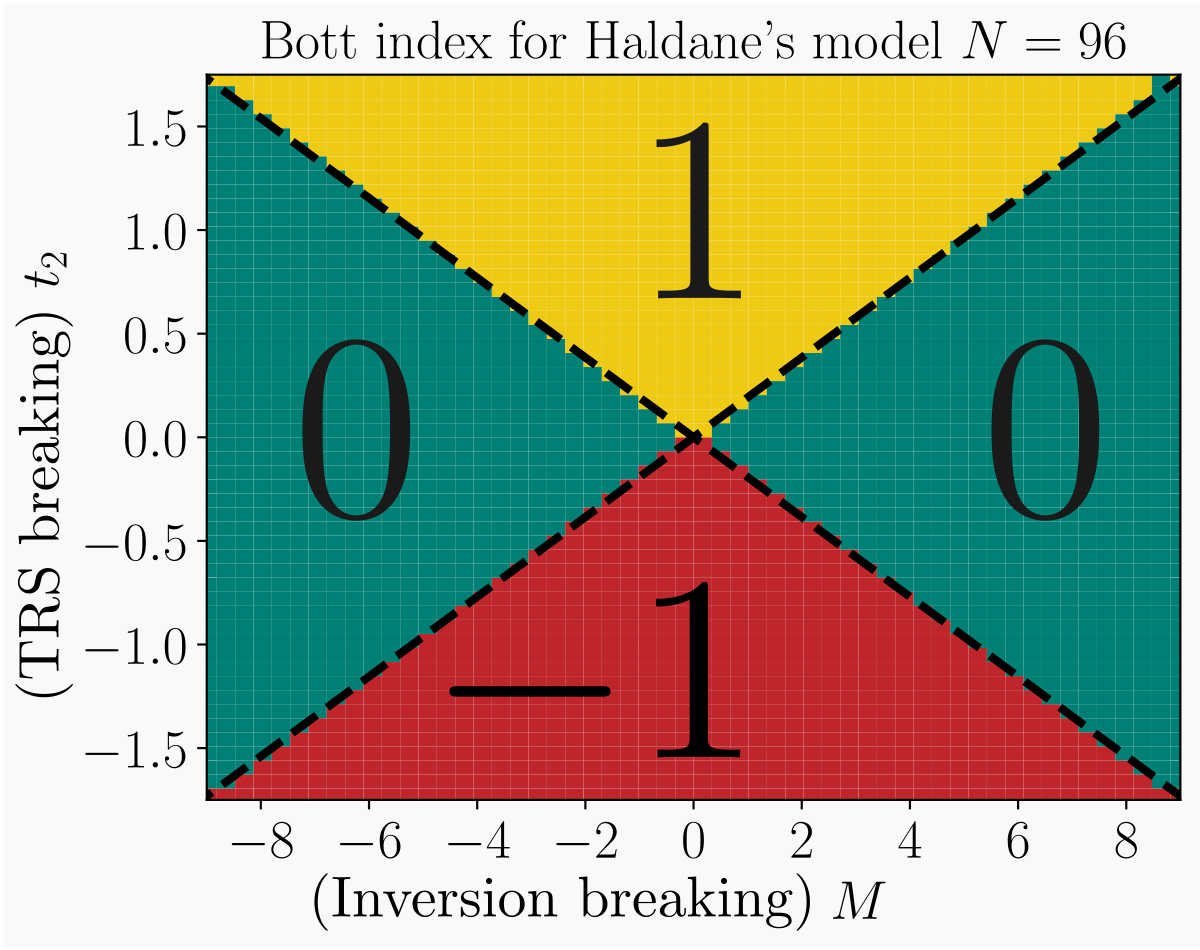
If $U$ and $V$ are almost unitary: $UU^{\dagger} \approx VV^{\dagger} \approx I$, then we can use another definition: \[ C_B = \frac{1}{2 \pi} \textrm{Im} (\textrm{tr} (\log (VUV^{\dagger} U^{\dagger}))) \]

Note that the Bott index is defined for a given energy

Our toolbox
  • Band diagram/Density of states
  • Nanoribbon
  • Inverse participation ratio
  • Chern number/Bott index
Topological photonic crystals

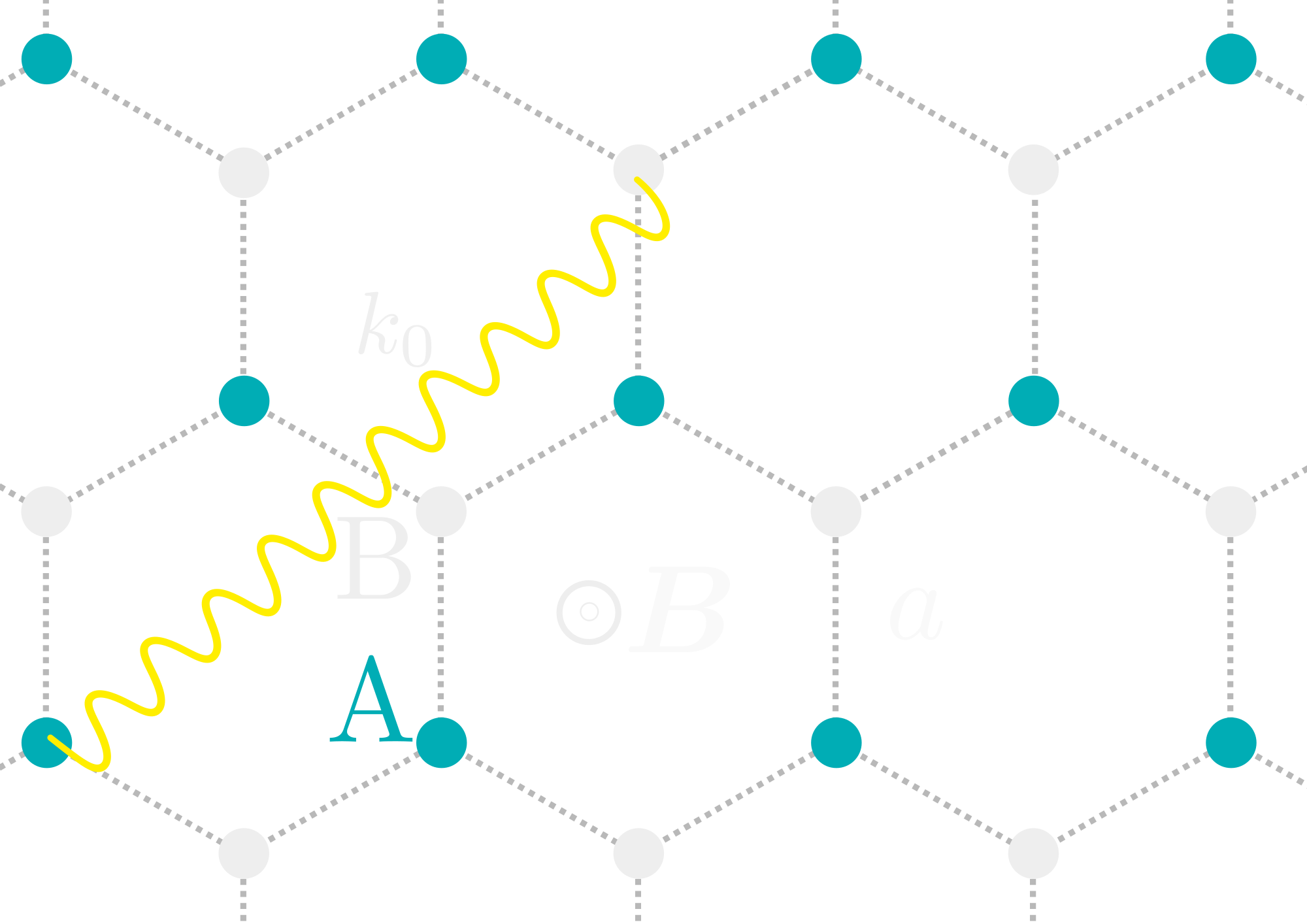
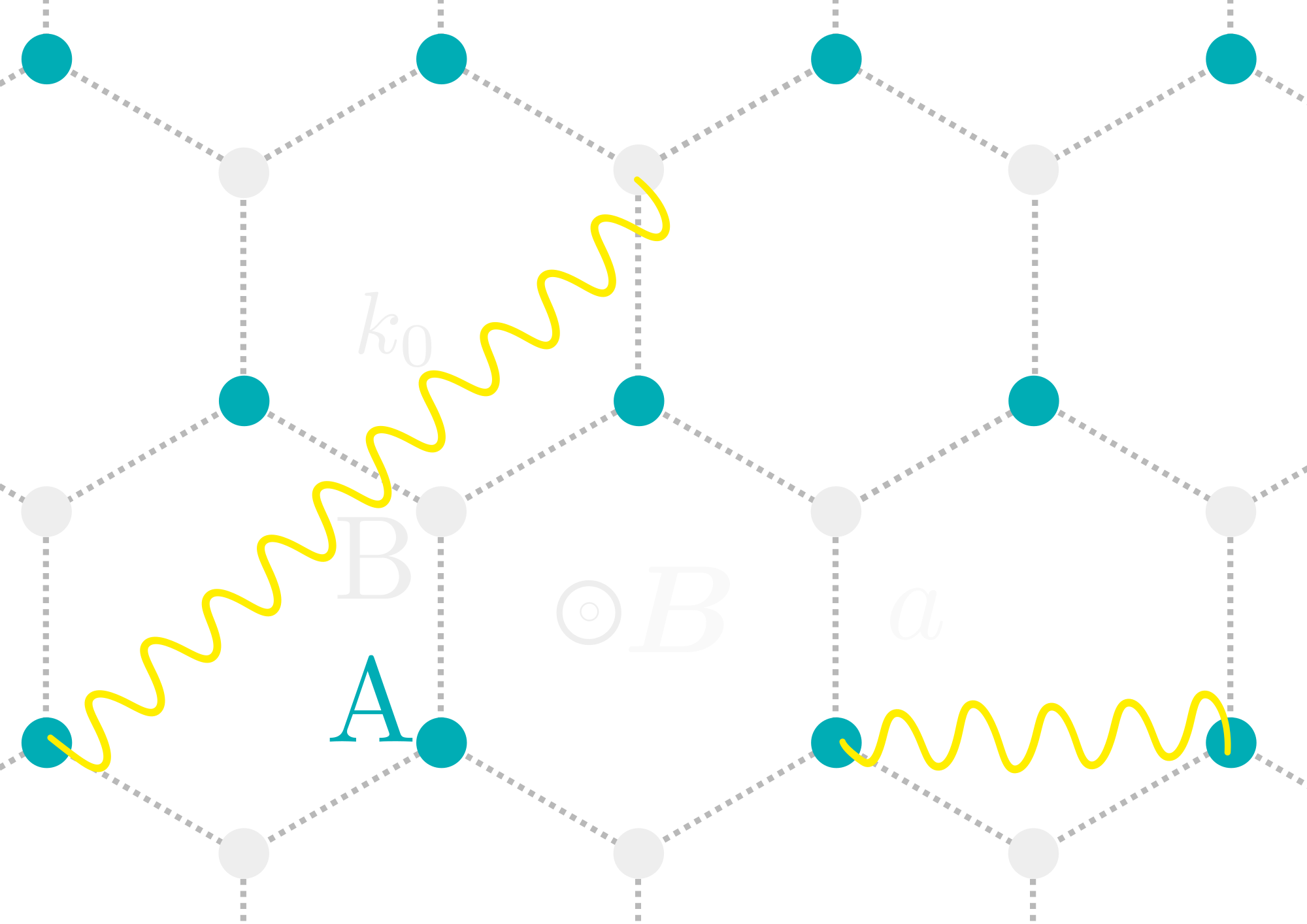
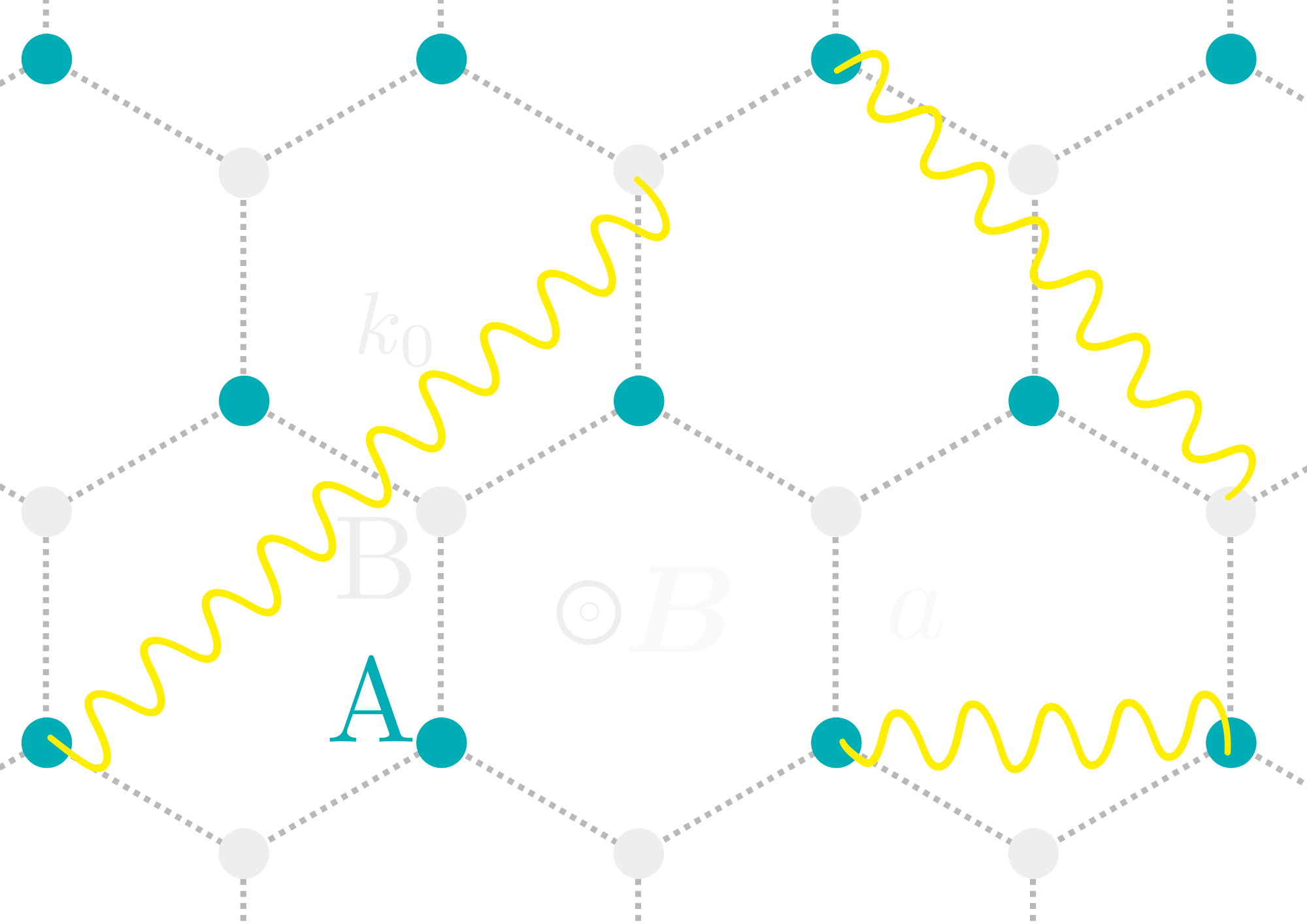
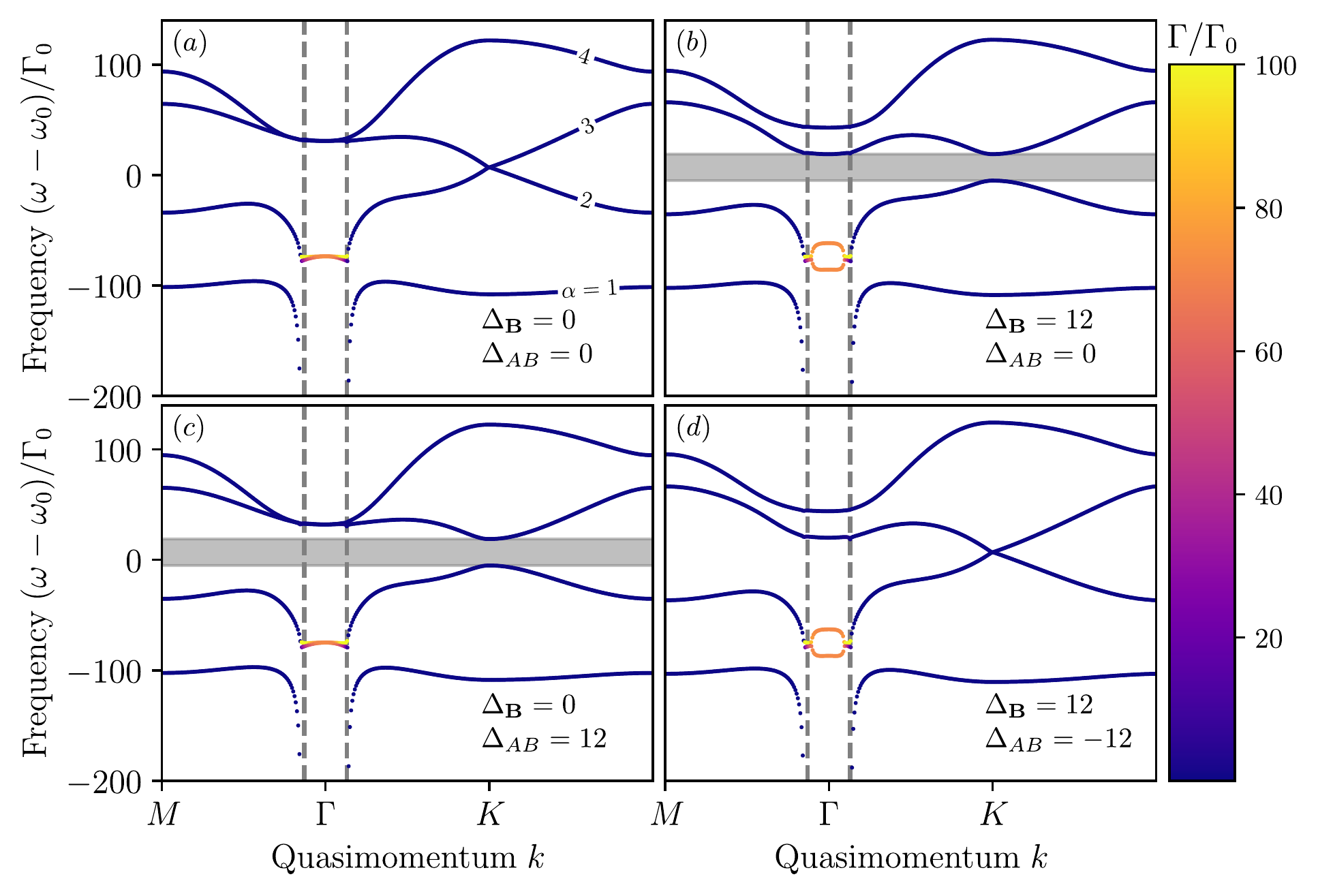
$$\begin{align*} H_{\mathrm{eff}} &=\sum_{n=1}^{N} \sum\limits_{m=-1}^1 \left(\textcolor{red}{\hbar\omega_{A,B}}+\textcolor{lime}{m g_e \mu_{B} |\bm{B}|} - \textcolor{cyan}{i\frac{\hbar\Gamma_{0}}{2}}\right) \left|e_{nm}\right\rangle\left\langle e_{nm}\right| \\ \nonumber &+\frac{3 \pi \hbar \Gamma_{0}}{k_{0}} \sum_{n \neq n'}^{N} \sum\limits_{m,m'=-1}^{1} \left( {\hat d}_{eg} \textcolor{yellow}{{\mathcal{G}} \left(\bm{r}_{n}, \bm{r}_{n'}\right)} {\hat d}_{eg}^{\dagger} \right)_{m m'} \left| e_{nm}\right\rangle\left\langle e_{n'm'} \right| \end{align*}$$

  • $\left|e_{nm}\right\rangle $ is the excited state of atom $n$ with a magnetic quantum number $m$
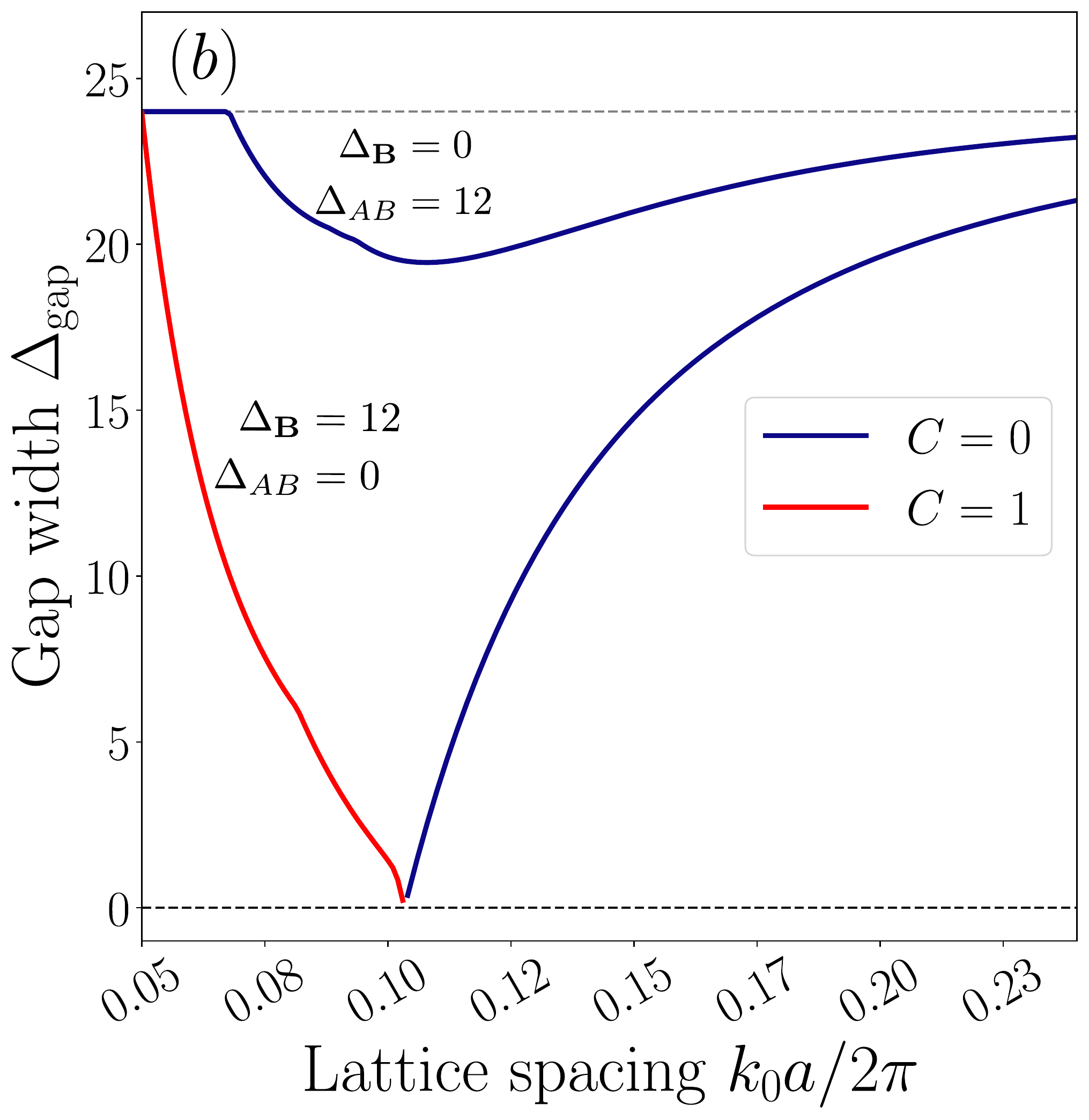
  • $k_0 = \omega_0/c$, $\omega_0 = (\omega_A + \omega_B)/2$ $\rightarrow \Delta_{AB} = (\omega_B -\omega_A)/2\Gamma_0$
  • $g_e \mu_B |\bm{B}|$ is the Zeeman shift $\rightarrow$ $\Delta_{\bm{B}} = g_e \mu_B |\bm{B}|/\hbar\Gamma_0$
  • $\Gamma_0$ is the radiative line width of an individual atom in the free space
  • \(\mathcal{G}\) is the dyadic Green's function describing the coupling of atoms by electromagnetic waves
    $$\mathcal{G}(\bm{r},\bm{r}') = -\frac{e^{ik \Delta r}}{r} \left( P (ik \Delta r) \mathbf{1}_3 + \frac{\Delta\bm{r} \otimes \Delta\bm{r}}{\Delta r^2} Q (ik \Delta r) \right) +\frac{\delta(\Delta\bm{r})}{3k_0^2}\mathbf{1}_3$$ $$\begin{align*} P (x) &=& 1 - \frac{1}{x} + \frac{1}{x^2} \\ Q (x) &=& - 1 + \frac{3}{x} - \frac{3}{x^2}\end{align*}$$

Spectrum of Light in a Quantum Fluctuating Periodic Structure, M. Antezza & Y. Castin, PRL. 103. 2009
Honeycomb lattice of atoms coupled via the EM field for $k_0 a = 2\pi × 0.05$
Width of the gap as a function of the Zeeman shift
How to know if a Bloch state is more on sites $A$ or $B$ ? $$\bm{\psi}_{\alpha}(\bm{k}) = (\bm{\psi}_{\alpha}^{A+}(\bm{k})\quad \bm{\psi}_{\alpha}^{A-}(\bm{k})\quad \bm{\psi}_{\alpha}^{B+}(\bm{k})\quad \bm{\psi}_{\alpha}^{B-}(\bm{k}))^T$$

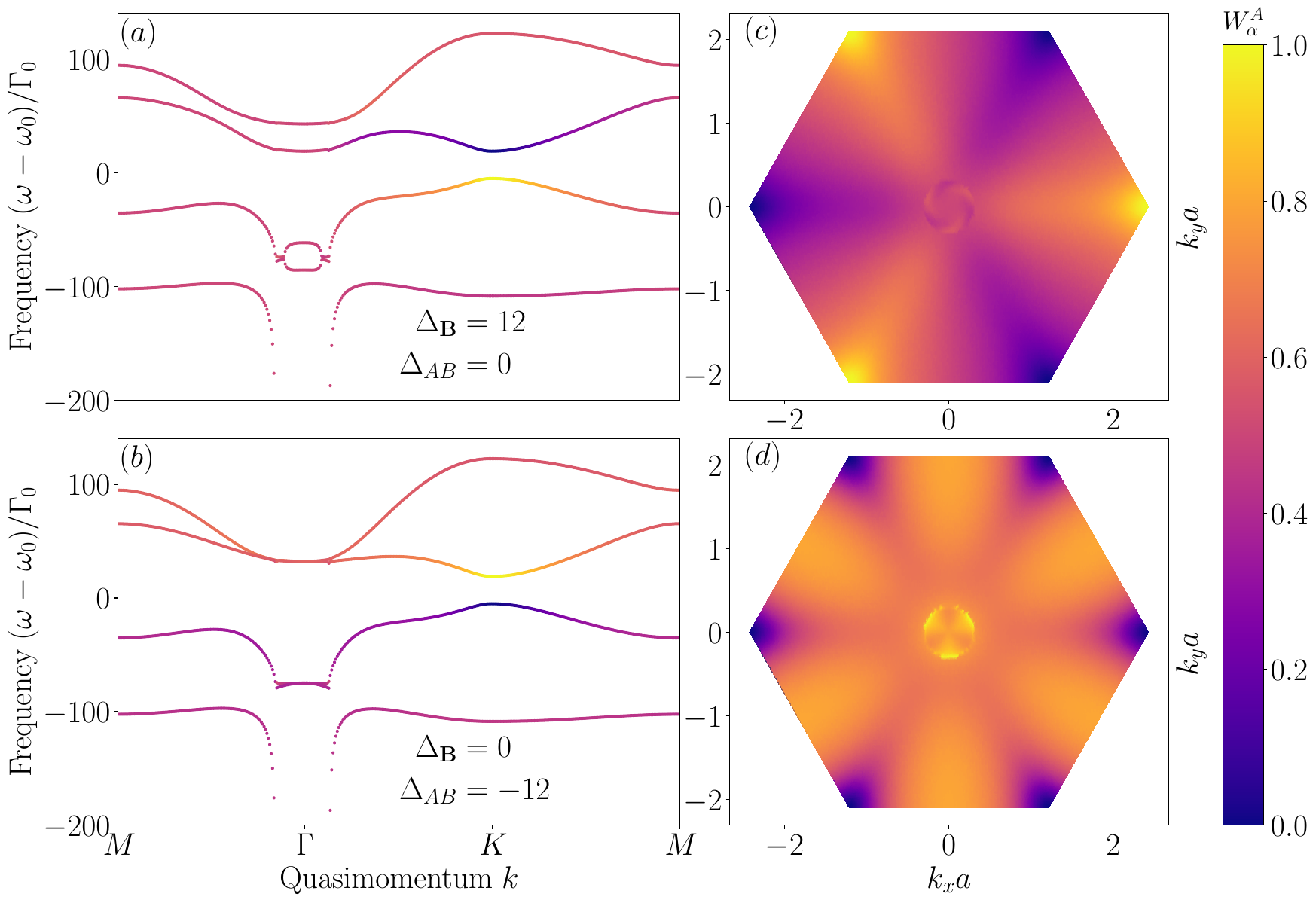
$$W_{\alpha}^A(\bm{k}) = \left|\bm{\psi}_{\alpha}^{A+}(\bm{k}) \right|^2 + \left|\bm{\psi}_{\alpha}^{A-}(\bm{k}) \right|^2$$

$$W_{\alpha}^A(\bm{k})+W_{\alpha}^B(\bm{k})=1$$

Band inversion
How can we observe the transition from a topological system to a trivial one?
The Impact of disorder
$$\delta r \in [0;Wa]$$
Comparison Chern / Bott
Disorder closes the gap

Topological Anderson Insulator, Jian Li et al., PRL. 102, 2009
The deformed honeycomb lattice
  • Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material, L. Wu & X. Hu, PRL 114, 2015
  • Topological Properties of Electrons in Honeycomb Lattice with Detuned Hopping Energy, L. Wu & X. Hu, S. Report, 2016
Remember the quantum spin Hall effect ?
  • Electric field: $$\bm{E}(\bm{r},t) = E_{\rho}(\bm{r},t) \bm{e}_{\rho} + E_{\varphi}(\bm{r},t) \bm{e}_{\varphi}$$
  • Magnetic field: $$\bm{B}(\bm{r},t) = B_z(\bm{r},t) \bm{e}_z$$
  • Poynting vector:$$\bm{S}(\bm{r}) = \text{Re} \left(\bm{E}(\bm{r}) \times \bm{B}^*(\bm{r}) \right)$$
  • Angular momentum: $$\begin{align*} \bm{J} &= \sum\limits_{n=1}^6 \nonumber \bm{r}_n \times \bm{S}(\bm{r}_n)\end{align*}$$
  
Change of base
Band diagram color-coded as a function of ressemblance to either $p$ or $d$ states
What topological index can be computed ?
Quantum Spin-Hall Effect and Topologically Invariant Chern Numbers, D. N. Sheng et al., PRL. 97, 2006
Robustness of the spin-Chern number, Emil Prodan, PRB. 80, 2009
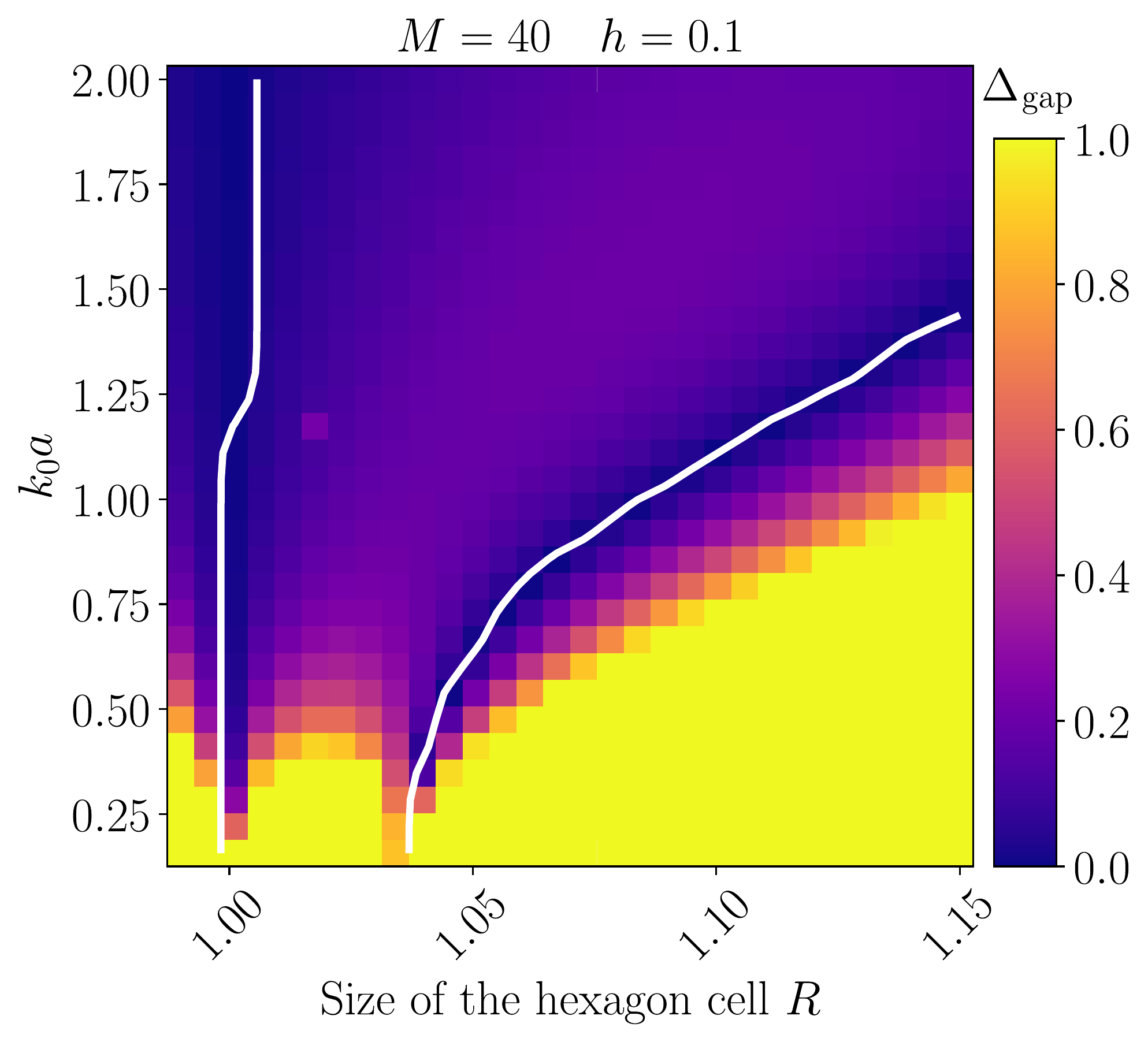
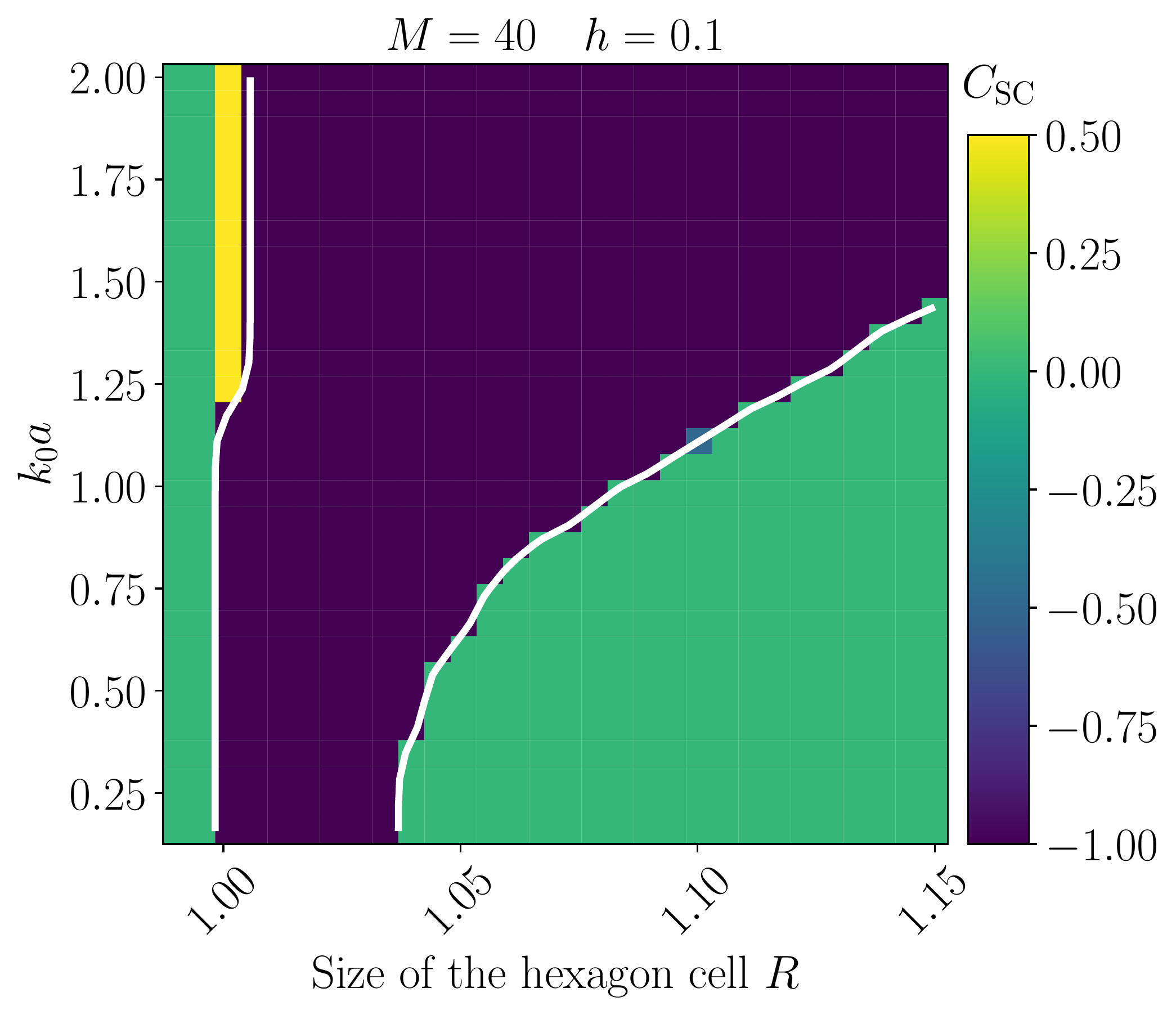
Image 1 Image 2
Conclusion and perspectives
Helical edge states propagation
In collaboration with L.A. Razo, G. Aubry and F. Mortessagne
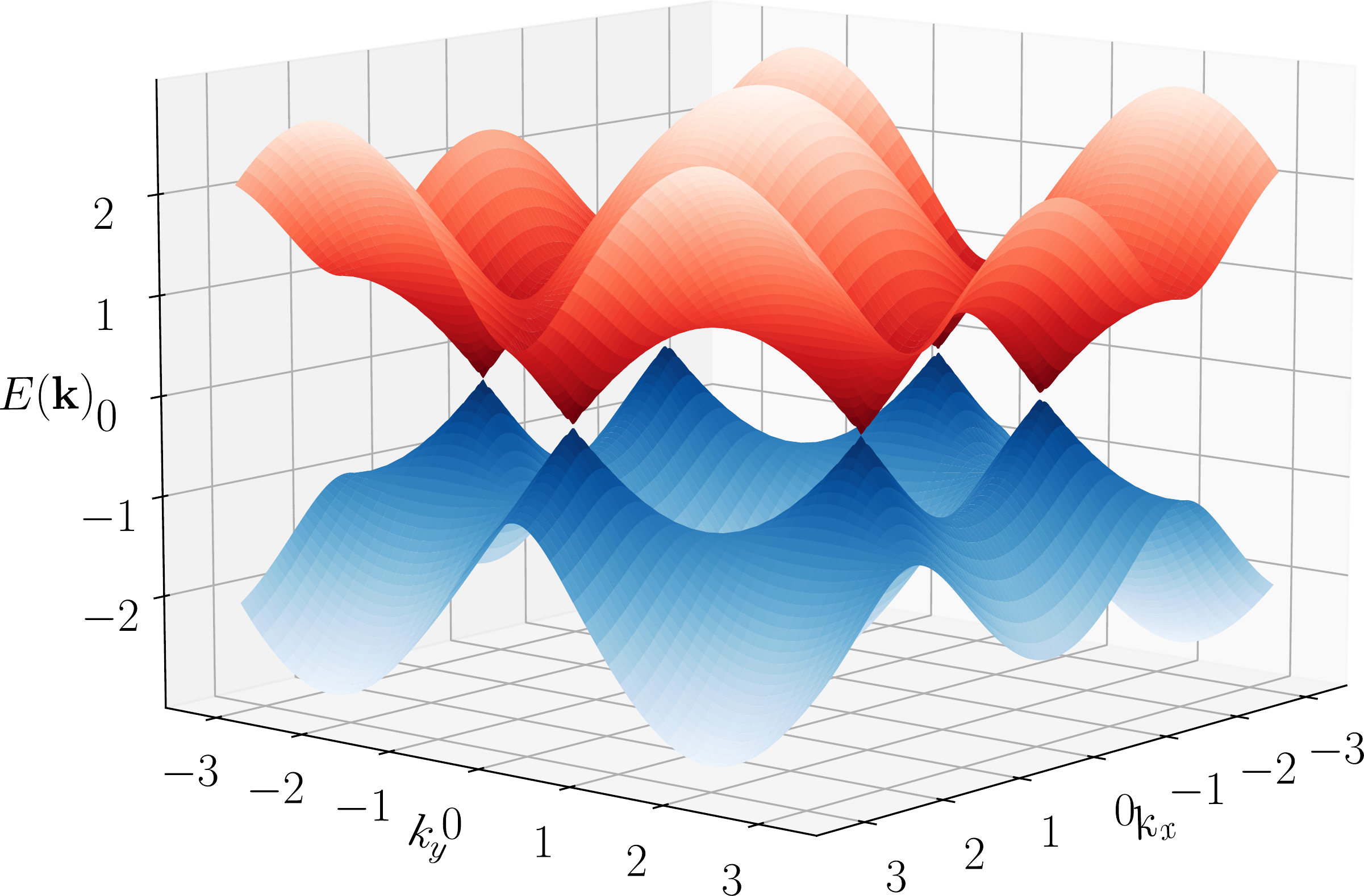
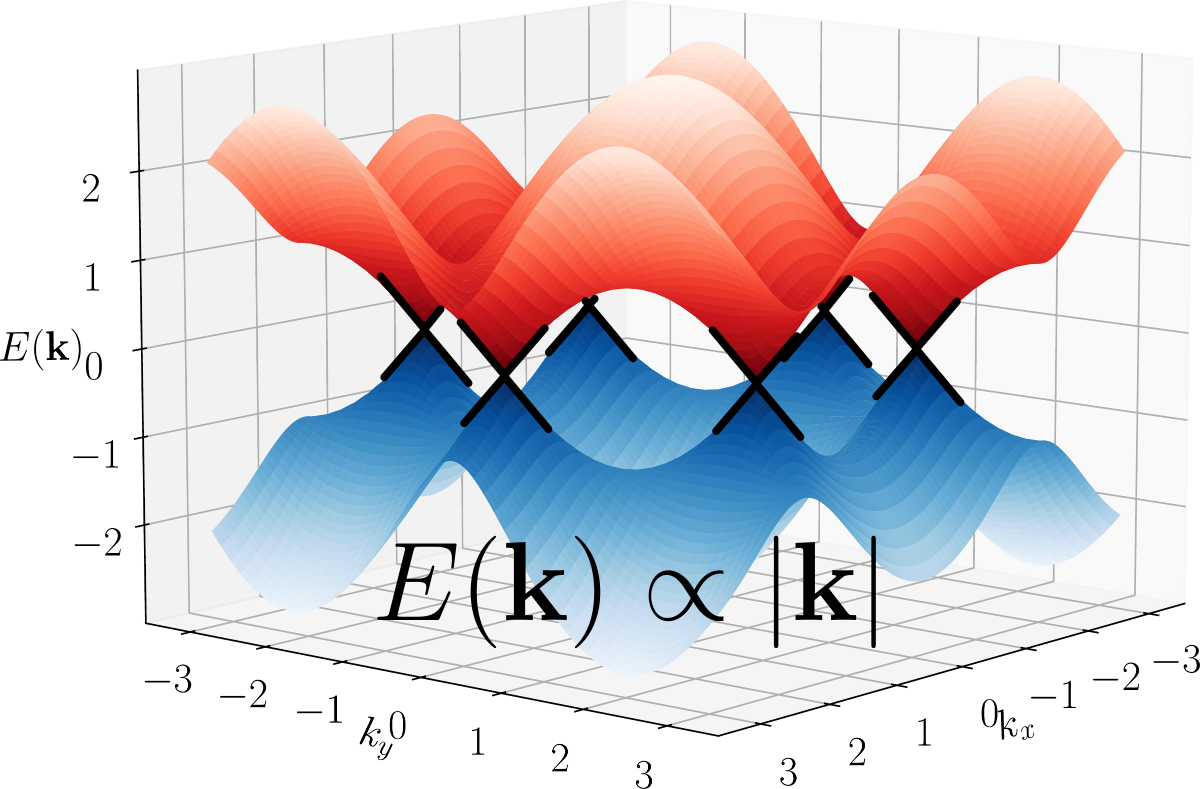
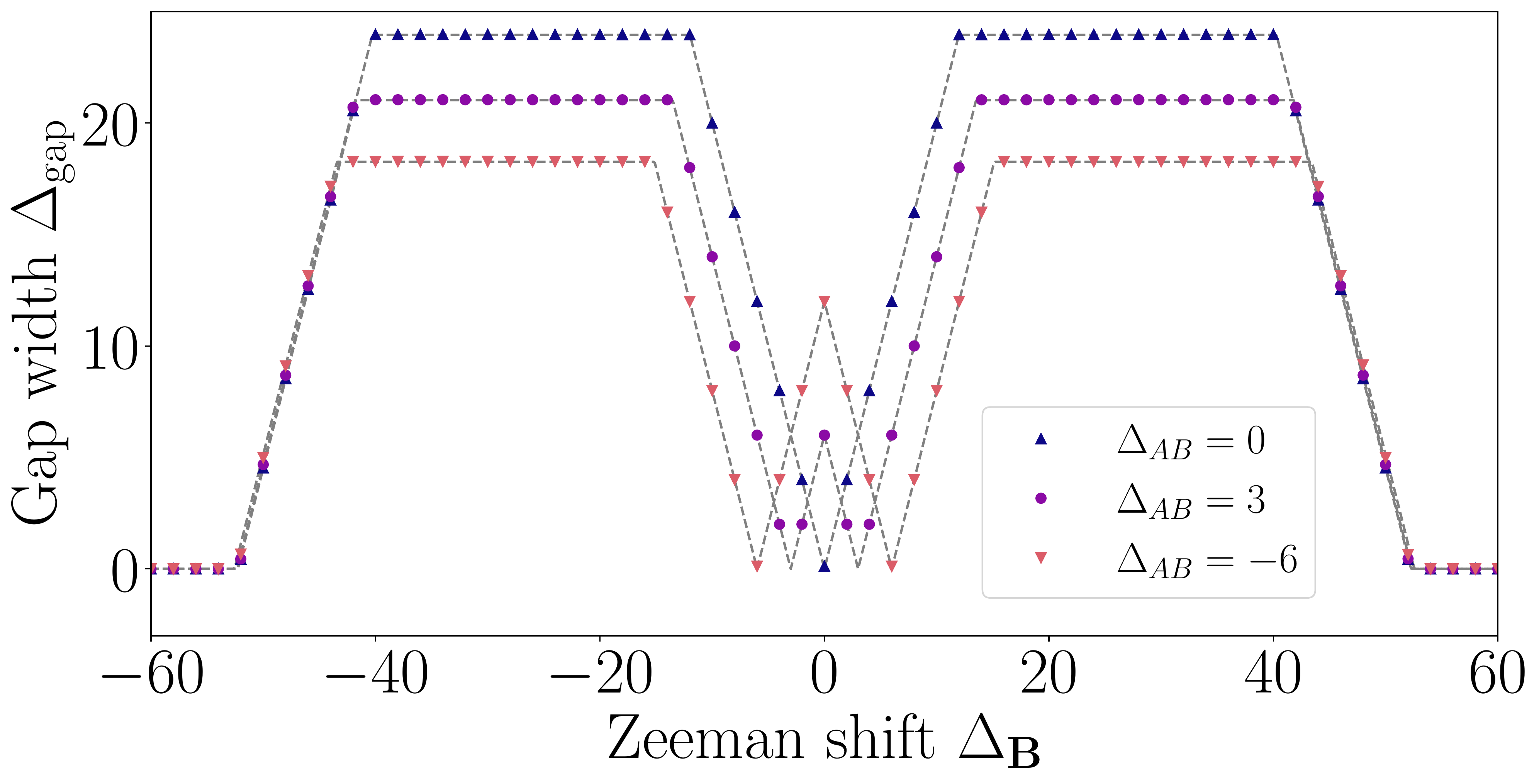
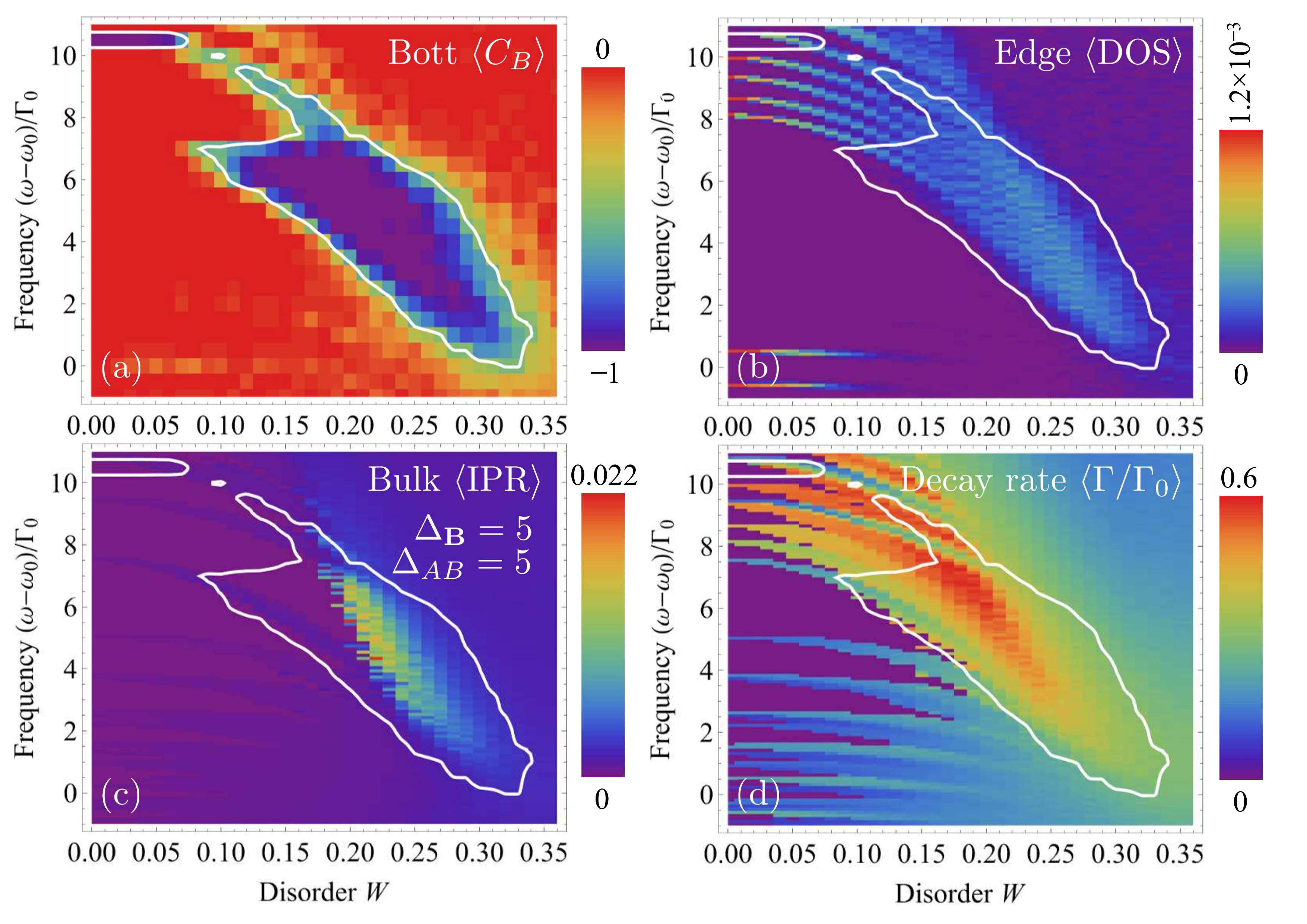
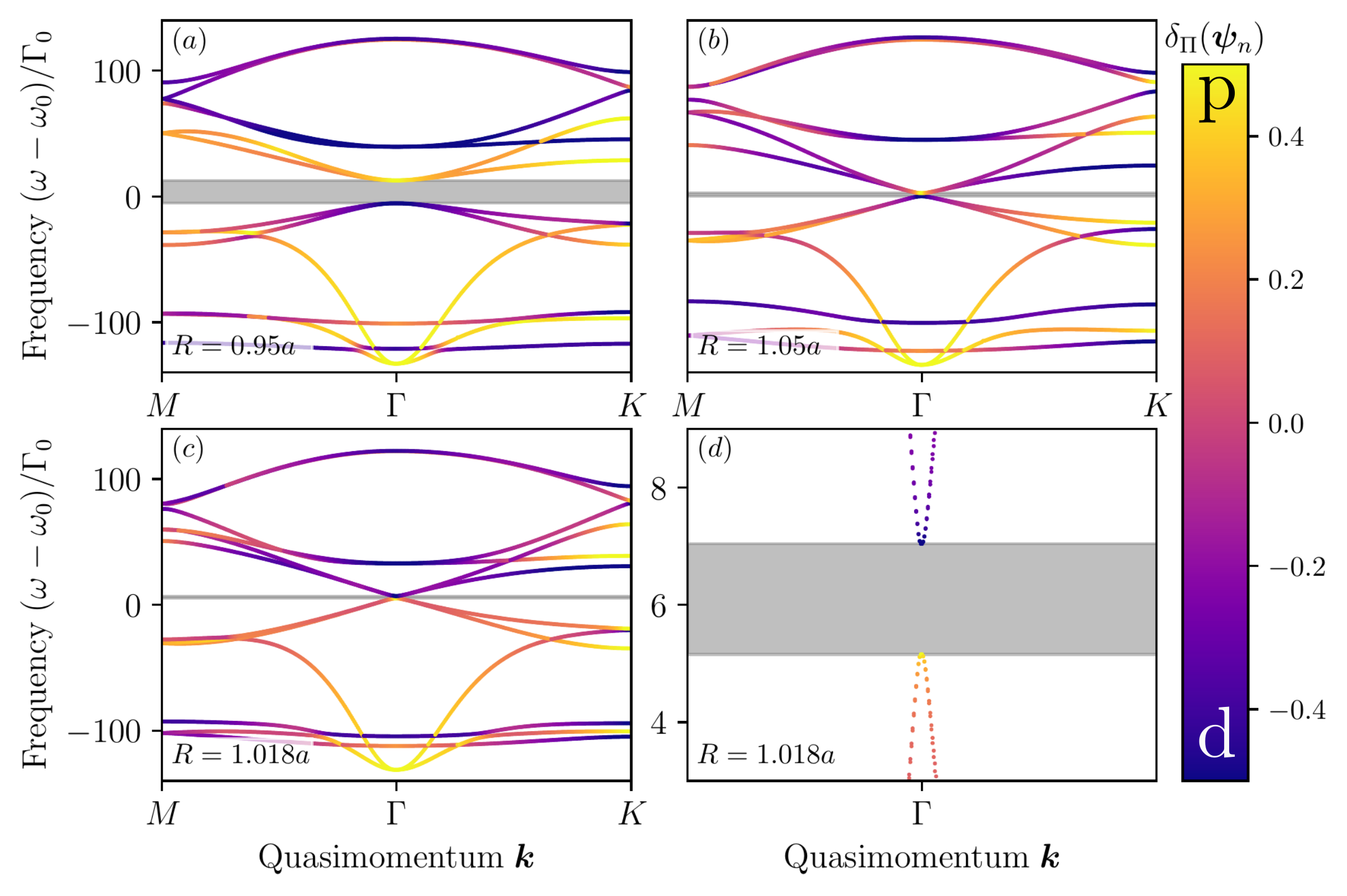
  • We established the band diagram of a honeycomb lattice consisting of atoms interacting via the electromagnetic field and studied the combined effect of time-reversal symmetry breaking and inversion one and thus, obtained formula for the width of the gap.
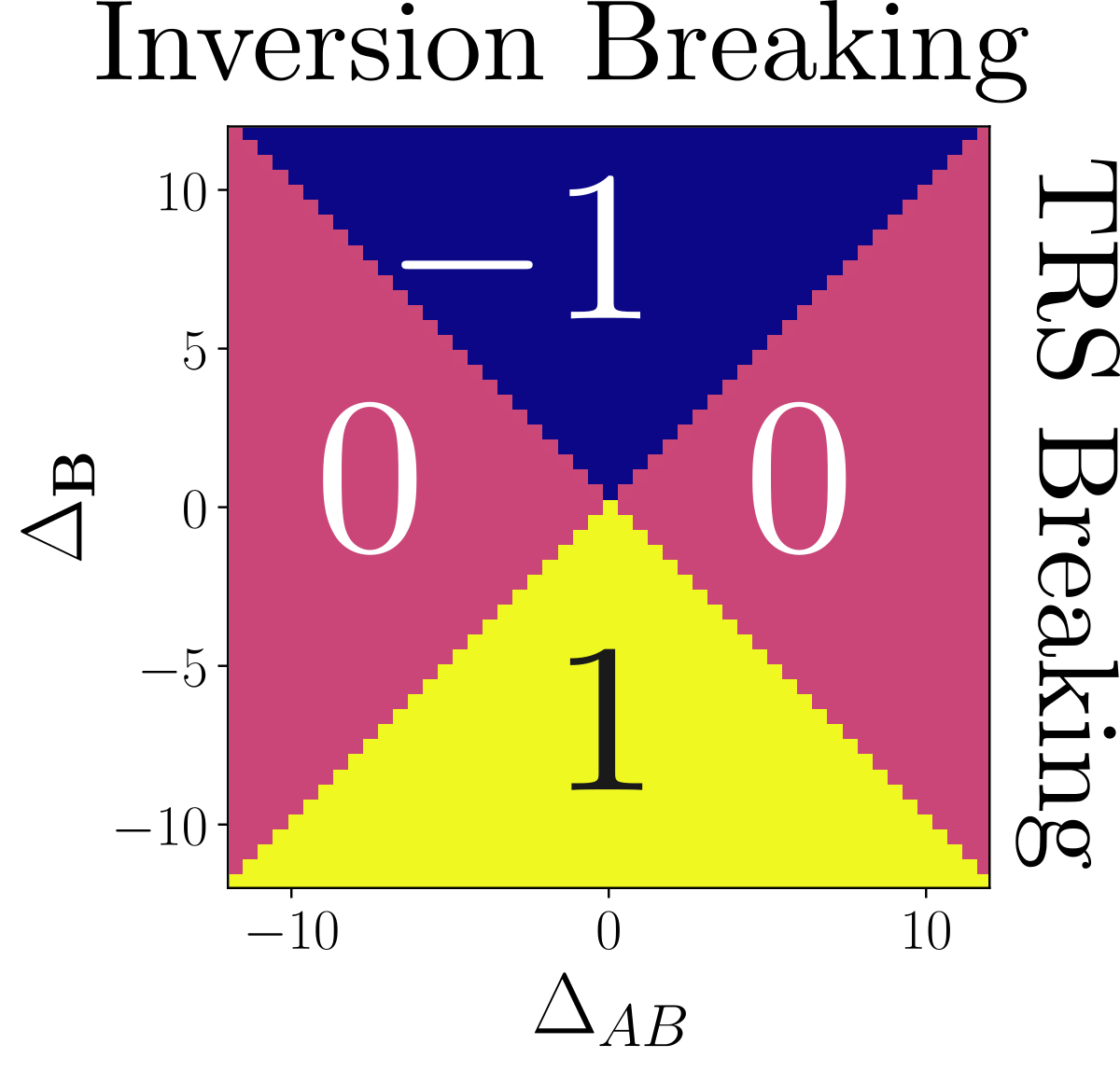
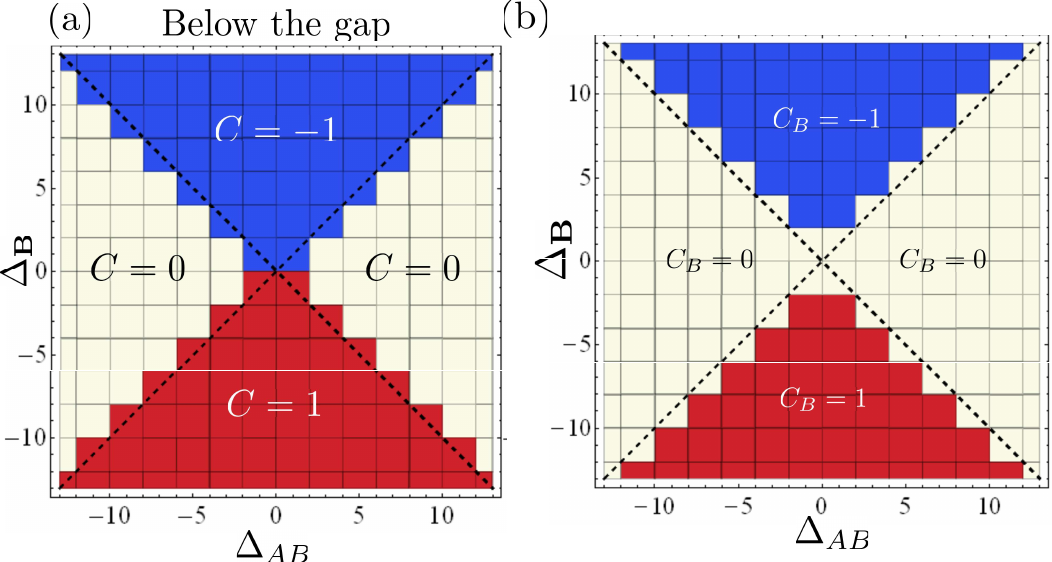
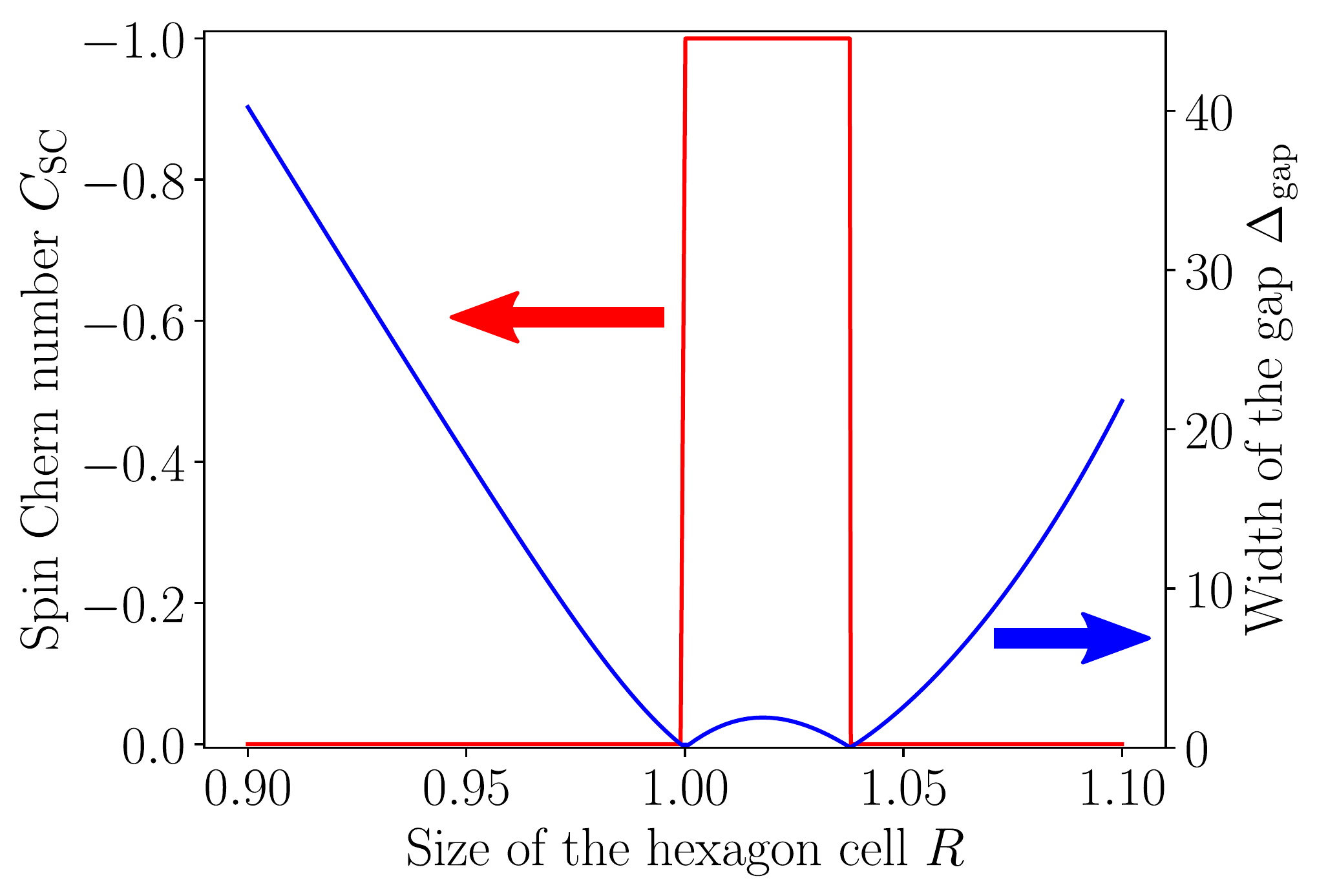
  • Using the Chern number, we also demonstrated that the gap is topological when the breakdown of time-reversal symmetry is stronger than that of the inversion one. We also demonstrated that the topological gap closes when transitioning to a trivial gap by increasing the lattice constant $a$.
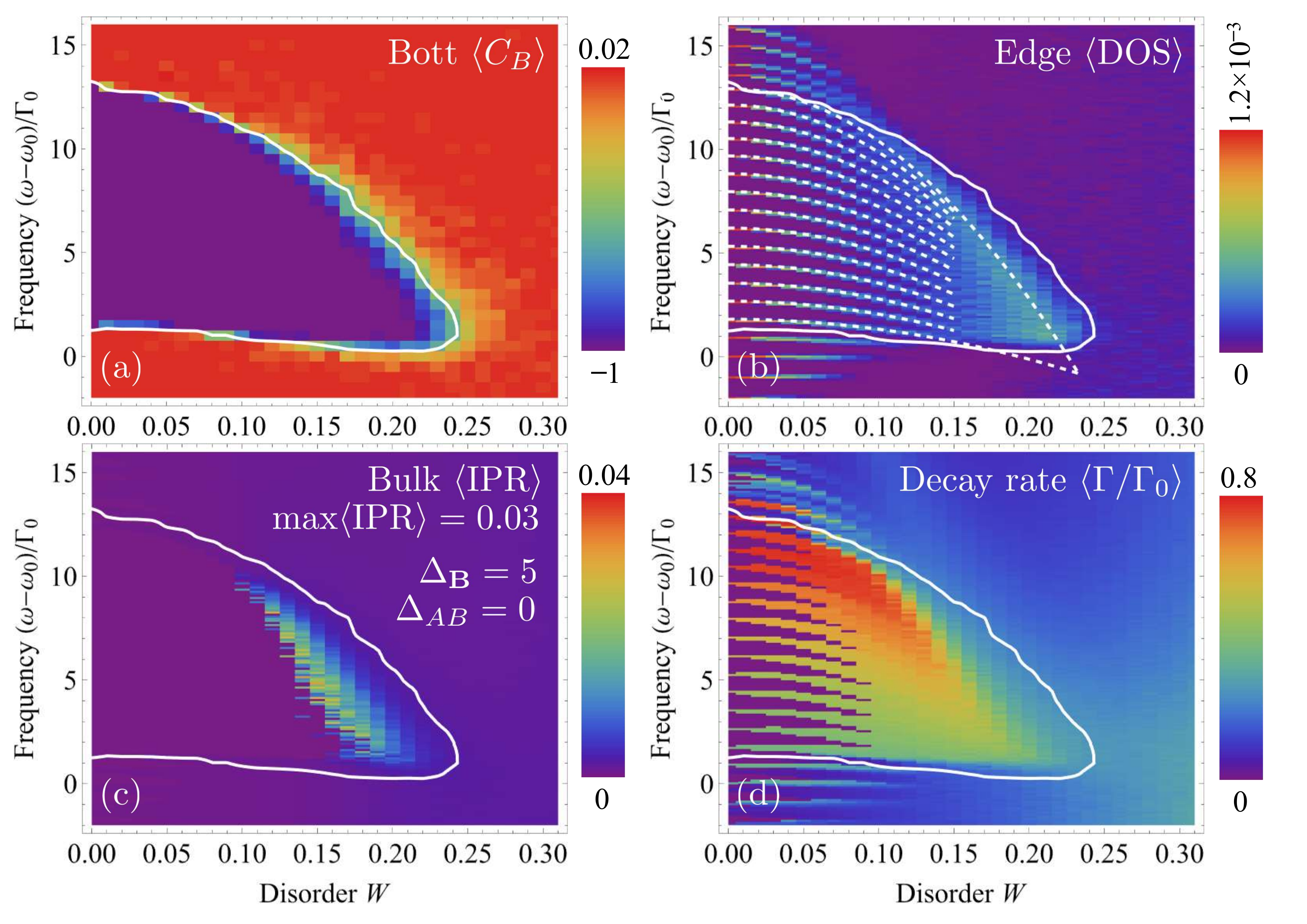
  • For a finite-size sample, using another topological invariant, the Bott index, we showed that the topological gap withstands disorder introduced by displacing the atoms randomly by distances up to 30% of the lattice constant $a$.
  • Furthermore, we show that if we perturb the positions of only one site out of two, the disorder can open a topological gap, a phenomenon also known as the “topological Anderson insulator”.
  • To circumvent the need for a magnetic field, we deformed the hexagonal cell and showed that a topological gap opens by computing the spin Chern number.
  • Topological transitions and Anderson localization of light in disordered atomic arrays, S. Skipetrov & P. Wulles, Phys. Rev. A 105, 043514 – 2022
  • Photonic topological Anderson insulator in a two-dimensional atomic lattice, S. Skipetrov & P. Wulles, Comptes Rendus. Physique, Volume 24 (2023) no. S3, pp. 39-54.
  • Topological photonic band gaps in honeycomb atomic arrays, P. Wulles & S. Skipetrov, SciPost Phys. Core 7, 051 (2024)
  • Light in deformed honeycomb lattice, P. Wulles & S. Skipetrov, in preparation
  • PyBott: a python package to compute the Bott index, P. Wulles & S. Skipetrov, in preparation
  • Helical edge states in arrays of dielectric cylinders, in preparation
It wasn't crystal clear ?